
Double Pendulum
 المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 20
الجزء والصفحة:
part 1 , p 20
 28-7-2016
28-7-2016
 1321
1321
Double Pendulum
The double pendulum consists of a mass m suspended by a massless string or rod of length l, from which is suspended another such rod and mass (see Figure 1.1).
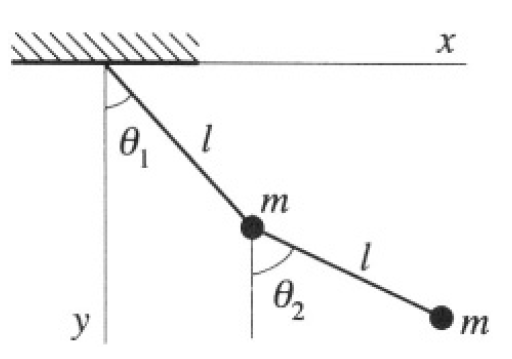
Figure 1.1
a) Write the Lagrangian of the system for θ1, θ2 << 1.
b) Derive the equations of motion.
c) Find the eigenfrequencies.
SOLUTION
a) For the first mass m, the Lagrangian is given by
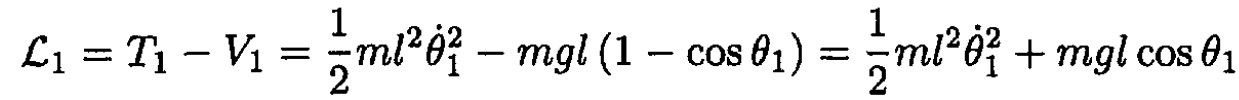
ignoring the constant mgl. To 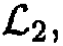 find introduce the coordinates for the second mass (see Figure 1.2):
find introduce the coordinates for the second mass (see Figure 1.2):
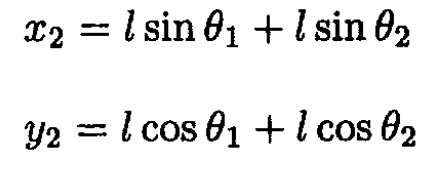
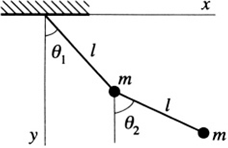
Figure 1.2
Now, 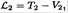 where
where
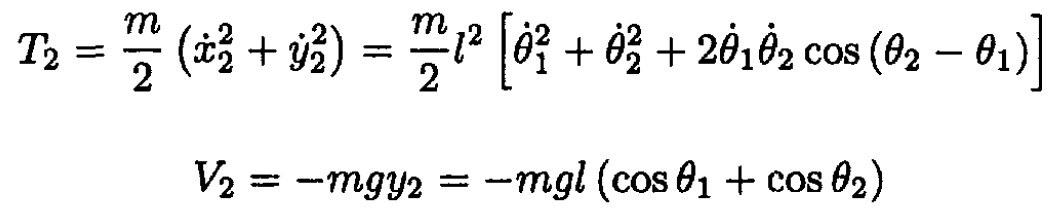
So
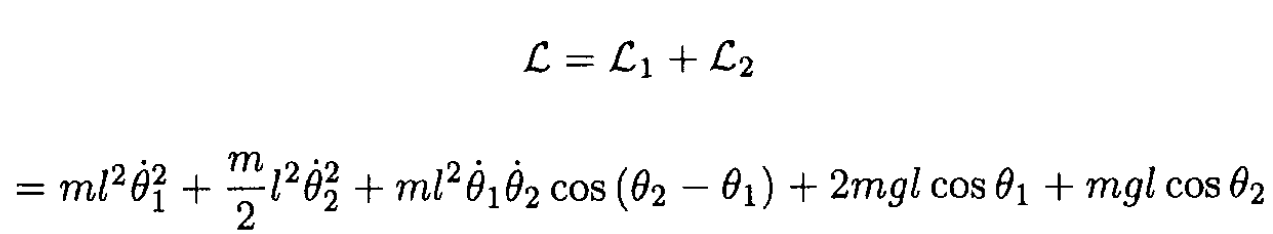
For θ1, θ2 << 1, we can take cos θ = 1- θ2/2. Denoting the frequency of a single pendulum by 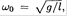 and eliminating superfluous constant terms, we obtain the Lagrangian in the form
and eliminating superfluous constant terms, we obtain the Lagrangian in the form
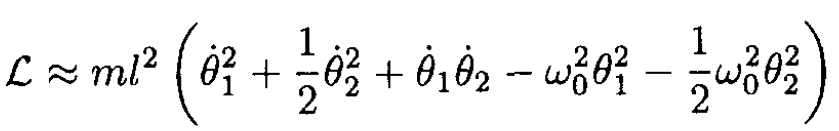 (1)
(1)
b) Using (1) we can write the equations of motion
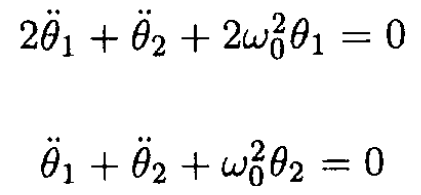 (2)
(2)
c) We are looking for solutions of (2) of the form
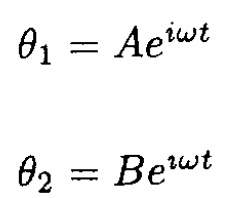 (3)
(3)
After substituting (3) into (2), we get a pair of linear equations in A and B
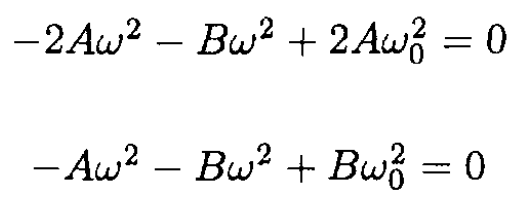 (4)
(4)
For nontrivial solutions of (4) to exist, we should have
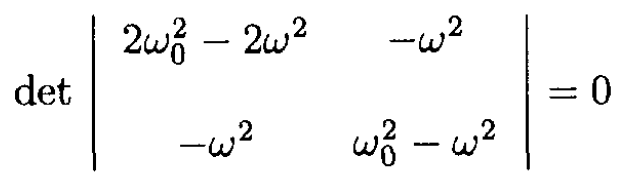 (5)
(5)
The eigenfrequencies are defined from
 (6)
(6)
Finally,
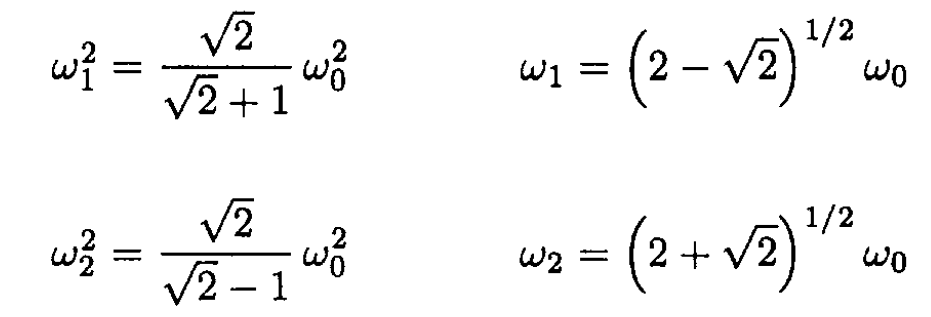 (7)
(7)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


