Cat and Mouse Tug of War

A rope is wrapped around a fixed cylinder as shown in Figure 1.1. There is friction between the rope and the cylinder, with a coefficient of friction

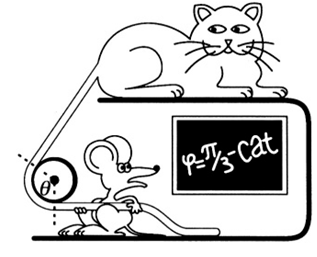
Figure 1.1

μ_i the angle θ₀ = π/3 defines the arc of the cylinder covered by the rope. The rope is much thinner than the cylinder. A cat is pulling on one end of the rope with a force F while 10 mice can just barely prevent it from sliding by applying a total force f = F/10.

a) Does the minimum force necessary to prevent the rope from sliding depend on the diameter of the cylinder?

b) Through what minimum angle about the cylinder should one mouse wrap the rope in order to prevent the cat from winning the game of tug of war?

SOLUTION

a) The straightforward solution is given in (b). However, to answer the first part, we can use dimensional analysis. The force f applied by the mice may depend only on the dimensionless coefficient of friction μ, the cylinder diameter d, and the force F :

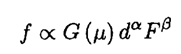
where G(μ) is some function of μ. It is obvious that it is impossible to satisfy this equation unless α = 0, so the force f does not depend on the diameter of the cylinder.

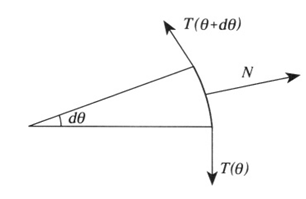
Figure 1.2

b) Consider an element of rope between angles θ and θ + dθ. The difference in tension dT between its ends equals dT = μN = μT dθ, where N is the normal force (see Figure 1.2). This equation has a solution: T = const . e^μθ. At θ = 0, T = f, and at θ₀ = π/3, T = F, so

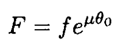(1)

From equation (1) we obtain the same result as determined in part (a), i.e., the force does not depend on the diameter of the cylinder. Similarly, if we have just one mouse, the minimum angle θ₁ of wrapping is found from

(2)

where f' = f/10 = F/100 is the force necessary for one mouse to keep the rope from slipping. From equation (1), we can also find the coefficient of friction μ:

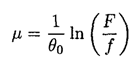
Then, from equation (2),