
Car down Ramp up Loop
 المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 7
الجزء والصفحة:
part 1 , p 7
 25-7-2016
25-7-2016
 1769
1769
Car down Ramp up Loop
A car slides without friction down a ramp described by a height function h(x) which is smooth and monotonically decreasing as x increases from 0 to L. The ramp is followed by a loop of radius R. Gravitational acceleration is a constant g in the negative h direction (see Figure 1.1).
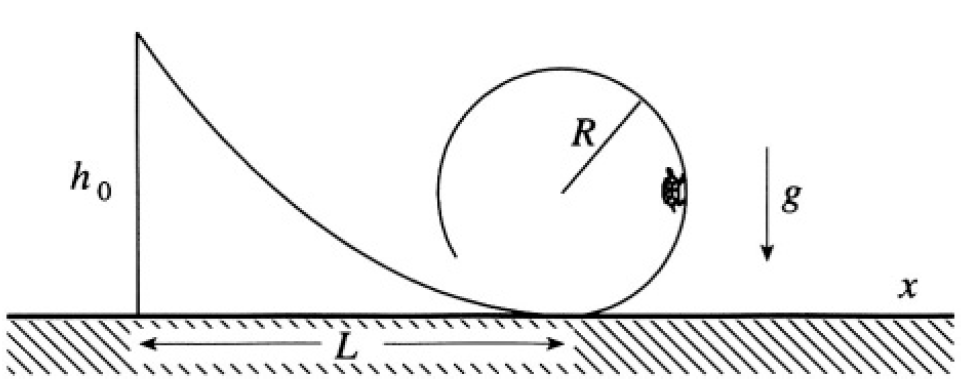
Figure 1.1
a) If the velocity is zero when x = 0, what is the minimum height h0 = h(0) such that the car goes around the loop, never leaving the track?
b) Consider the motion in the interval 0 < x < L before the loop. Assuming that the car always stays on the track, show that the velocity in the x direction is related to the height as
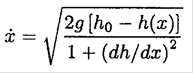
c) In the particular case that show that the h(x) = h0[1- sin (πx/2L)] time elapsed in going down the ramp from (0, h0) to (L, 0) can be expressed as 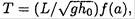 where a ≡ πh0 /2L, and write f(a) as a definite integral. Evaluate the integral in the limiting case h0 >> L and discuss the meaning of your answer.
where a ≡ πh0 /2L, and write f(a) as a definite integral. Evaluate the integral in the limiting case h0 >> L and discuss the meaning of your answer.
SOLUTION
a) Since there is no friction, we have from energy conservation
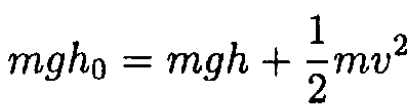
Where v is the velocity of the car and m is its mass (see Figure 1.2). At any point of the ramp, the normal force of the ramp on the car should
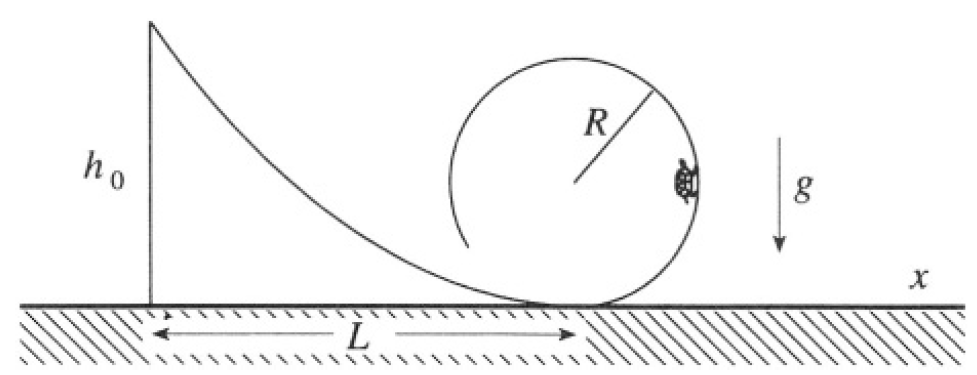
Figure 1.2
be nonzero; otherwise, the car will leave the ramp. Obviously, the critical point is the top of the loop, x = L, where the velocity is minimal and gravity and centrifugal forces are antiparallel. For this point,
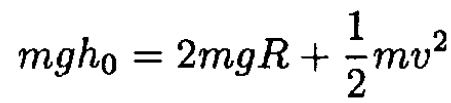 (1)
(1)
The minimum height h corresponds to a velocity v = vmin at this point, enough to provide a centrifugal acceleration equal to the gravitational acceleration:
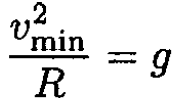
Substituting this into (1) yields
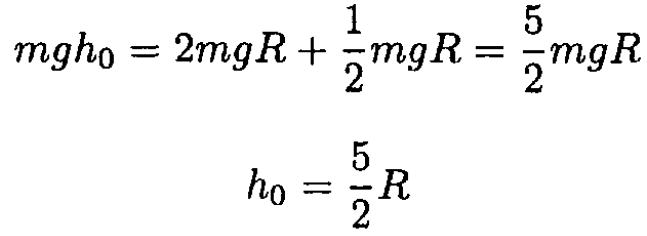
b) Consider a point on the ramp 0 < x < L. The velocity at this point is defined by
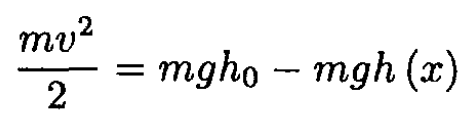 (2)
(2)
Where v2 may be written
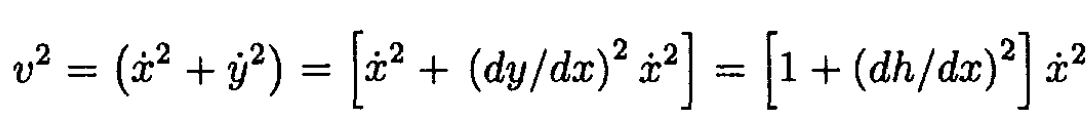 (3)
(3)
where the slope of the curve dy/dx is given by the derivative of the height function dh/dx Substituting (3) into (2) results in
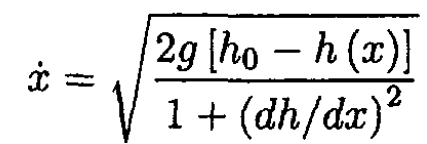
c) Now consider h(x) = h0 [1-sin (πx/2L)]. Rewrite the solution to (b) as
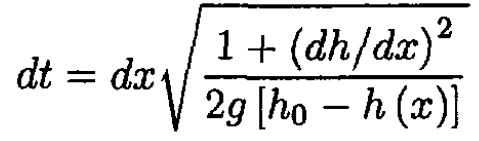
The time T to travel to x = L can be expressed by the integral
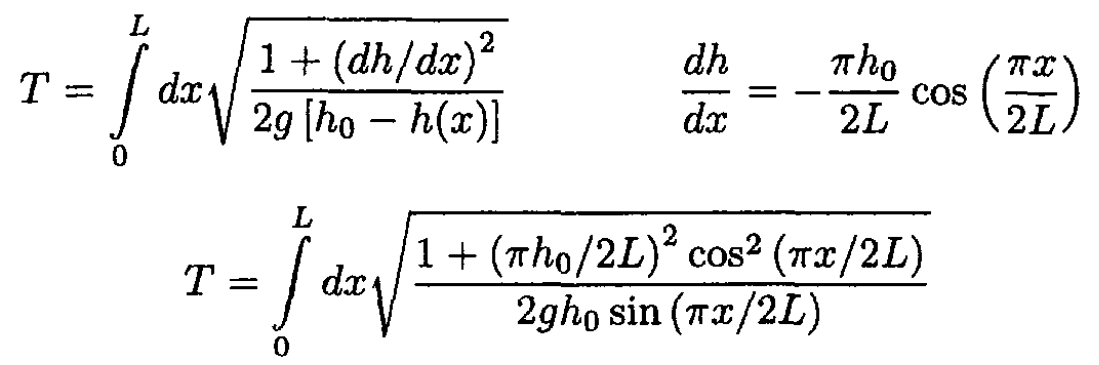
Letting ζ = πx/2L and a ≡ πh0 /2L, we obtain
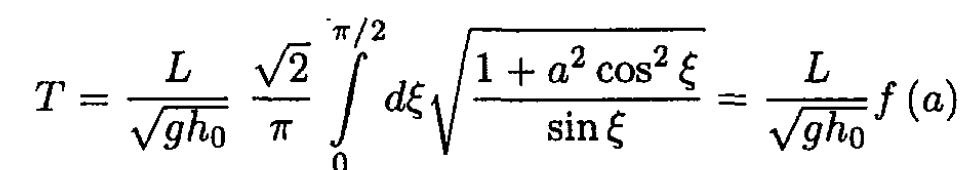
where
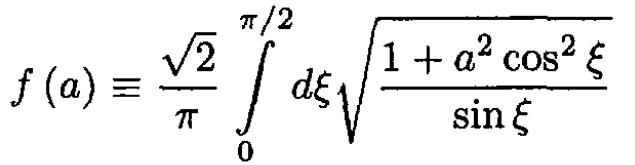
In the limiting case of h0 >> L, or a << 1, let us write the integral in the form
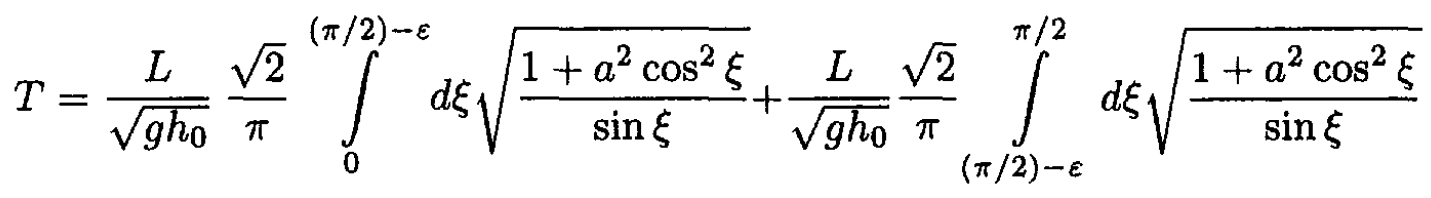
We can neglect 1 compared to a2 cos2 ζ for the region from 0 to (π/2) – ε, with 1/a < ε << 1. Then we have
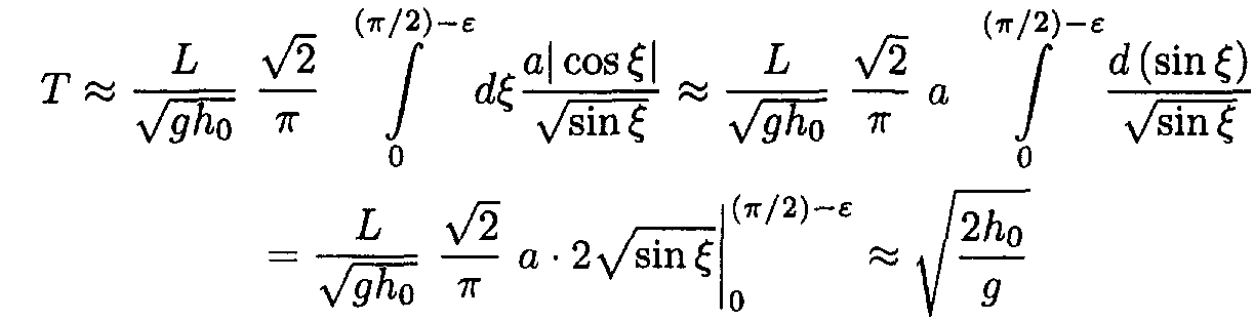
This corresponds to free fall from the height h0, where gT2/2 = h0.
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


