
Positronium and Relativistic Doppler Effect
 المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 1 , p 39
الجزء والصفحة:
part 1 , p 39
 13-7-2016
13-7-2016
 1585
1585
Positronium and Relativistic Doppler Effect
An electron e- and a positron, e+, each of mass me, bound with binding energy εb in positronium, annihilate into two photons.
a) Calculate the energy, momentum, velocity, and frequency of the photons.
b) The positronium with velocity v moves away from the observer in the lab and annihilates as shown in Figure 1.1. Give the frequency of the photon as measured by the observer and calculate its frequency in terms of the frequency in the positronium rest system (Relativistic Doppler Effect).

Figure 1.1
SOLUTION
a) The two photons will have momenta p of the same magnitude (but opposite sign), so their energies ε are also the same:
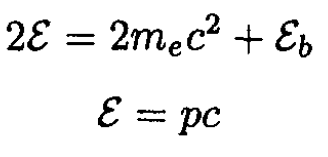
where we have chosen their momenta to be along the x axis. From these formulas we can find
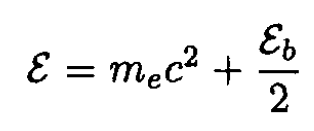 (1)
(1)
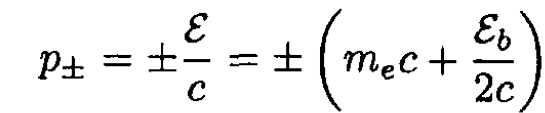 (2)
(2)
The frequency of the photons is
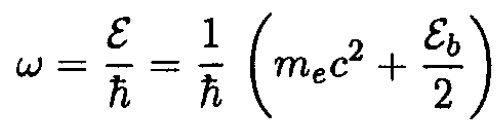 (3)
(3)
The velocity of the photon is, of course, u = ± c.
b) To find the velocity and the frequency of the photon in the lab frame we can use the Lorentz transformations for momentum and energy for the photon that is registered by the observer (with momentum p- from (2)):
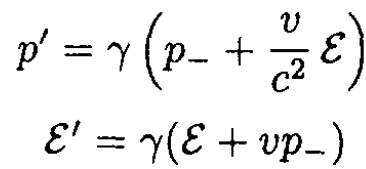
where ε, p are the energy and momentum of the photon in the rest frame, and ε', p' are the energy and momentum of the photon in the observer’s frame.
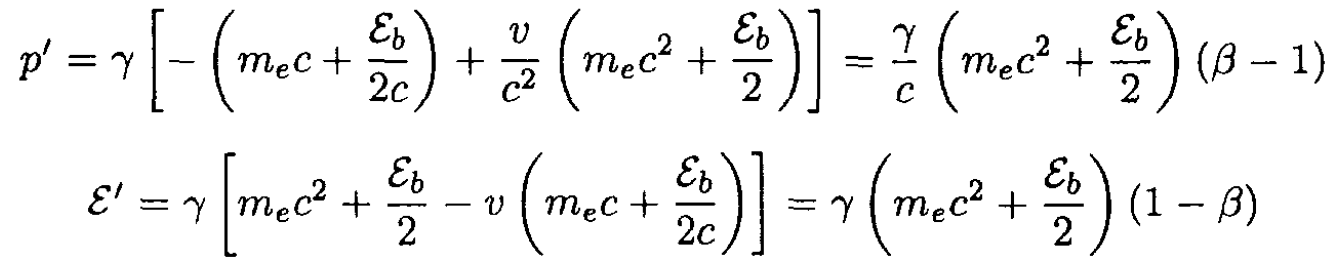
so the velocity of the photon in the observer’s frame is u' = p'c2/ε' = - c, which of course is what one would expect. The frequency of the photon measured by the observer is
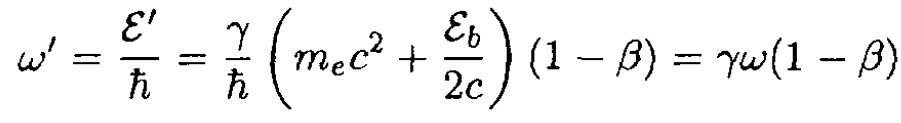
where we substitute ω from (3) of (a). So the original frequency is redshifted to
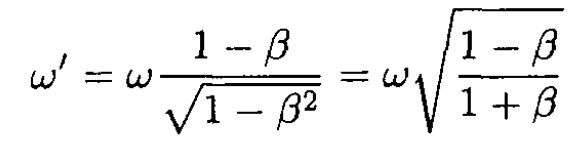
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


