اسلوب خط الاتجاه المعدل بالعوامل الموسمية

كيف يؤثر العامل الموسمي في الاتجاه ؟

الطريقة الاولى: اما ان يؤثر العامل الموسمي في الاتجاه بنسبة ثابته تضاف الى الاتجاه بغض النظر عن يمة الاتجاه وتطلق على هذا النوع من التغيرات الموسمية (Additive Seasonal Variations) وتكتب الصيغة العامة للتنبؤ المعدل في حالة اضافة العامل الموسمي للاتجاه كما يلي

الطريقة الثانية:  واما ان يؤثر العامل الموسمي في الاتجاه بنسبة متغيرة اي قيمة العامل الموسمي تضرب بقيمة الاتجاه . وتطلق على نوع من المتغيرات الموسمية .

والمثال التالي يوضح كيفية تطبيق هذا الاسلوب مثال (3-6)

قرر احد منتجي الاقمشة الحرير الصناعي استخدام اسلوب خط الاتجاه لتنبؤ الطلب على الحرير الصناعي خلال عام 2001 . من خلال الخبرة الماضية فان هذا المنتج يعلم بان الطلب على الحرير الصناعي يتغير حسب فصول السنة وكما يظهر في الجدول (3-10) . والمطلوب تنبؤ الطلب للفصول الاربعة لعام 2001 بأسلوب خط الاتجاه المعدل بالعوامل الموسمية مرة بطريقة الضرب ومرة بطريقة الاضافة .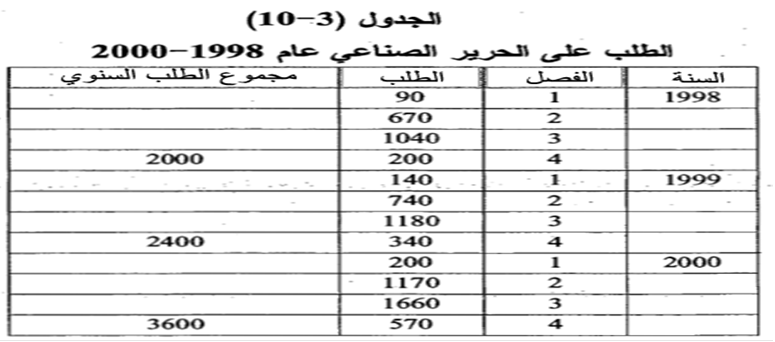

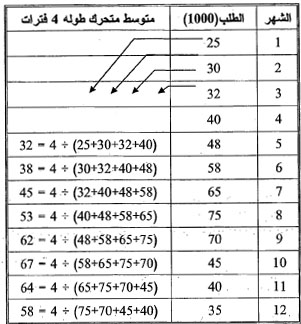
الحل:

1- بحساب قيمة ثوابت معادلة الاتجاه العام (a ) و (b ) فإن معادلة خط الاتجاه ( 3-9 ) هي: y= 302+ 56× 

2- وباستخدام المعادلة السابقة نتمكن من إجراء تنبؤ للفصول الأربعة من عام 2001 التي سيكون  رتيبها في السلسلة × هو   13    و 14 و15  و 16  للفصول الأول والثاني والثالث والرابع من عام 2001 على التوالي:

نلاحظ أن التنبؤ الفصل يغير معدل بالعوامل الموسمية لكل فصل وكما يلي:

3- حساب العوامل الموسمية يحسب الوسط الحسابي للطلب السنويD  بقسمة مجموع الطلب السنوي على عدد فصول السنة، أي

حيث أن Dt  = الطلب الفصلي الحقيقي وبالتعويض فإن الوسط الحسابي للطلب السنوي لعام 1998 هو:

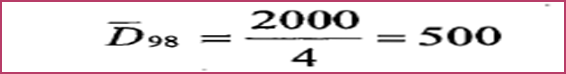
ب- يحسب العامل الموسمي لكل فصل وذالك بقسمة الطلب الحقيقي في كل فصل على متوسط الطلب السنوي كما في القاعدة الاتية 

وبتطبيق هذه القاعدة يمكن الحصول على العوامل الموسمية لعام 1998 كالاتي

وبأعاده نفس الخطوات على السنتين الاخريين يمكن الحصول على النتائج الاتية

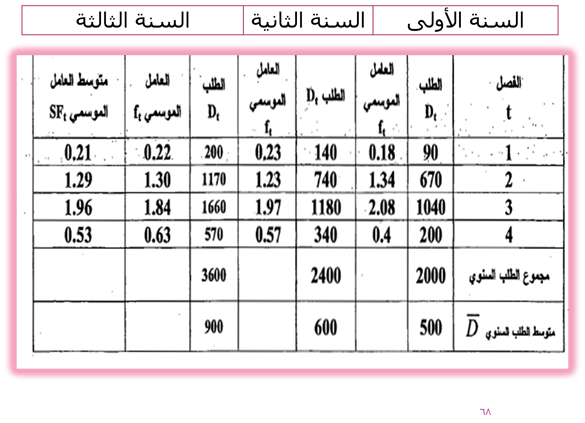
ج. حساب متوسط العامل الموسمي ( sft )  لكل فصل وذلك بجميع العوامل الموسمية (ft ) لكل فصل وقسمة على عدد السنوات (وهي ثلاث في هذا المثال ).

ولإجراء ذلك نطبق القاعدة التالية:

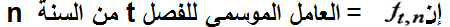
وبتطبيق القاعدة السابقة نحصل على العامل الموسمي للفصول الأربعة لعام 2002 وكما يلي:

وبنفس الطريقة تم الحصول على العوامل الموسمية للفصول الأخيرة وكما يظهر في نتائج التحليل السابقة.

4. يعدل التنبؤ من الخطوة ( 2) بالعوامل الموسمية السابقة وكما يلي:

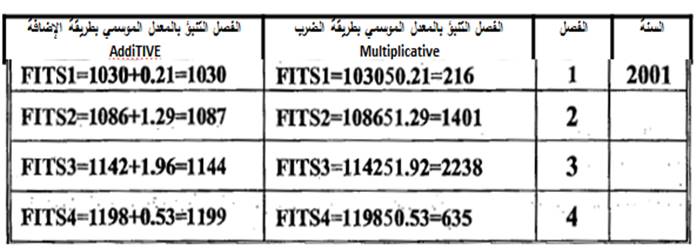والآن أي الطريقتين أفضل؟ تعديل الاتجاه بطريقة الضرب أم بطريقة الجمع ؟  إن الإجابات على هذا السؤال تتطلب معرفة مقدار خط التنبؤ ( Forecast  ) الذي ينتج عن كل طريقة.