Non-linear electrophoresis

Electrophoresis can be visualized by an analogy.  Imagine spherical glass marbles rolling down a slope in a tank  of syrup.  The  profile  of the slope could be described by plotting  contour  lines.  The marbles would move very slowly because of the viscosity of the syrup and so they  would essentially acquire no momentum.  As a result they would always  move  in the direction of the slope, even if this was to change its direction,  i.e. the locus of any  one marble would always be at right  angles to  the  contour lines. The locus would reflect the direction of the force vector acting upon each marble and the magnitude of the  force  would be inversely proportional to the spacing between the contour lines. In electrophoresis, the equivalent of contour lines would be is voltage contours and the  loci  of ions  undergoing electrophoresis  would correspond to  field lines,  which are always at right  angles to  the is voltage contour lines.

In most forms of electrophoresis,  the  field lines are straight  and the is voltage contours are evenly  spaced.  In the  marbles-in-syrup analogy, this is equivalent to the marbles moving down a straight plane  surface, inclined at an angle to  the  horizontal.  However,  deviating  from  this straight and narrow  approach  can be instructive  and one can pose a number of “what if?” questions to probe one's own insight into electrophoresis, e.g.

 What if the gel was of increasing cross-section, i.e. either conical  or wedge-shaped?

 What if the gel was not straight, but went through a 90  bend?

 What  if the  gel  had  a hole  cut  in  it  (say  if there  was  a  pillar passing through the gel)?

These questions have been explored theoretically and empirically by Dennison . If the  gel  were  conical  or  wedge-shaped, the  voltage  gradient (dV/dx) would be steeper at the narrow end and shallower at the wider end.  The net result is that the migration of slower ions would be increased, as they would spend more time in the steep part  of the  gradient,  whereas that  of faster ions would be slowed as they would reach the shallower parts   the gradient more  quickly.  Normally,  in  gel  electrophoresis  the  mobility  of ions is a logarithmic  function  of their molecular weight,  so that  small ions are separated better than  larger ions.  In a wedge-shaped gel the relationship is made more linear. Although this result has not found much utility in the separation  of proteins,  wedge gels have  proved  useful in the  separation  of nucleic acids.  In DNA sequencing gels, a greater number of bases can  be  sequenced in  a  wedge gel  compared  to  a  straight-sided slab gel, and the  separation  of plasmids is also improved  in wedge-shaped gels. The wedge-gel concept  has been extended to preparative electrophoresis by Rolchigo and Graves, and to  IEF by An empirical analysis of electrophoresis around corners was done by Dennison (Fig. 1).  Around a comer, the  is voltage contours remain as straight lines but become closer together on the inside of the corner than on the outside,  rather like the  steps in a spiral  staircase.  As  a result, the voltage gradient is steeper on the  inside of the  corner  and the proteins on this side will accelerate when negotiating the corner.  By contrast, the  isovoltage contours are further apart on the outside of the corner and the proteins will  slow down.  The  net  result  is  that  the  protein band will become skewed as it rounds the comer.  Negotiating a second comer in the  opposite  direction  does not undo  the distortion.

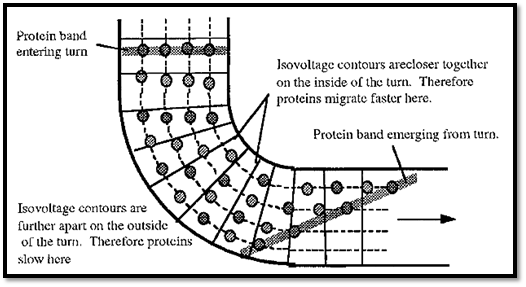
Figure 1.  The effect of a bend in the gel upon electrophoretic behaviour in PAGE.

Electrophoresis around a circular obstruction in the gel is shown in Fig. 2.  The isovoltage contour lines (shown as solid lines) can easily be visualized, remembering the  fact that  they  are always at  right  angles to the field lines (shown as dotted lines).  An interesting conclusion was drawn from  these  experiments,  i.e. that  the  equations describing the behaviour of ions undergoing electrophoresis  are identical  to  those describing the  irrotational  flow of an ideal incompressible  fluid.  Ideal fluid behaviour was previously considered to  be only  an  abstract  concept; in an ideal fluid the molecules have no momentum.

If one  has  a  playful  nature,  the  shapes  of the  voltage  gradient  surfaces can be visualized on a visit to  the  beach.  Pouring loose beach-sand down a slope,  in which  a  circular  obstruction  has  been  placed,  will  form  a contoured surface around the obstruction.  In  ones  minds  eye  one  could imagine this surface  in  the  tank  of syrup  and visualize the  movement  of marbles down the surface  it will be found to be identical to the behaviour of ions  around the  circular  obstruction  shown  in  Fig.  2! To summarize, the following points can be noted about non-linear electrophoresis:

• Field lines pass smoothly around comers  or obstructions  and resemble

“streamlines”.

• Ions will migrate along field lines, i.e. the  field lines will represent  the loci of migrating ions.

• Isovoltage  contour lines are always at right angles to the field lines.

• Ions will migrate  quickly where the  isovoltage  contour  lines are close

together (i.e.  where the voltage gradient is steep)  and slowly where  the isovoltage contour lines are far apart (i.e. where the voltage gradient is shallow).

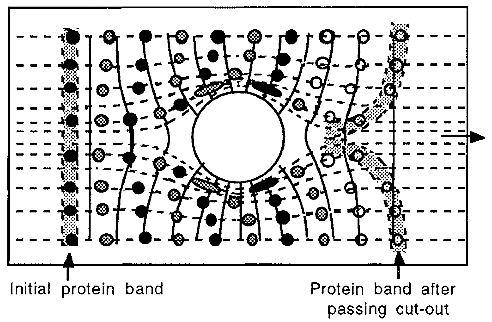
Figure 2.  The effect of a circular hole in an electrophoresis gel.

References 

Dennison, C. (2002). A guide to protein isolation . School of Molecular mid Cellular Biosciences, University of Natal . Kluwer Academic Publishers new york, Boston, Dordrecht, London, Moscow .

Dennison, C., Lindner, W.  A.  and Phillips, N.  C.  K.  (1982) Nonuniform field gel electrophoresis. Anal. Biochem.  120, 12-1 8 (1 982).

Dennison, C., Phillips, A. M. and Nevin, J. M. (1983) Nonlinear gel electrophoresis: an analogy with ideal fluid flow. Anal. Biochem.  135, 379-382.

Ansorge,  W.  and Labiet, S. (1 984)  Field  gradients  improve  resolution  on  DNA sequencing gels. J. Biochem. Biophys. Methods 10, 237-243.

Bonicelli, E., Simeone, A., deFalco, A., Fidanza, V. and La Volpe, A.  (1983) An agarose gel resolving a wide range of DNA fragment lengths. Anal. Biochem.  134, 40-43.

Olsson, A., Moks, T., Uhlen, M.  and Gaal, A. B.  (1984) Uniformly spaced banding pattern in DNA sequencing gels by use of field-strength gradient.  J. Biochem. Biophys. Methods  10, 83-90.

Rochelle, P. A., Day, M.  J.  and Fry, J.  C.  (1986) The use of agarose wedge-gel electrophoresis for resolving both small and large naturally occurring plasmids. Lett. Appl. Micro. 2, 47-51.