المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | نقطة الانقطاع Discontinuities Points |
 2767
 02:15 صباحاً
التاريخ: 27-12-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 366|
أقرأ أيضاً
التاريخ: 23-5-2019
1708
التاريخ: 24-3-2019
1586
التاريخ: 22-4-2019
1904
التاريخ: 29-4-2018
1792
|
وتسمى نقط عدم الاتصال ففي النقط التي لا يكون عندها الاقتران متصلاً كأن يكون الاقتران عندها غير معرف أو نهايته غير موجود وقيمته عندها لا تساوي نهايته أي ان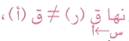 
، عندما أ نقطة النقطاع , وتتواجد هذه النقط في أغلب الأحيان في أطراف الاقترانات المحدودة حيث النهاية غير موجودة في الأطراف نقط القفز في الاقتران أكبر عدد صحيح أي عند ما تكون قيمة الاقتران عدداً صحيحاً أو اصفار مقام الاقتران النسبي ويمكن ان تكون نقط التغيير في التعريف في الاقترانات المنشعبة مثل .
|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|
