المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | قاطع التمام Cosecant |
 4835
 10:44 صباحاً
التاريخ: 22-11-2015 |
المؤلف : صالح رشيد بطارسه 
الكتاب أو المصدر : معجم الرياضيات 
الجزء والصفحة : 224-225|
أقرأ أيضاً
التاريخ: 9-2-2017
1118
التاريخ: 26-11-2015
1208
التاريخ: 9-2-2017
1056
التاريخ: 13-2-2017
1010
|
يرتبط قاطع التمام بالزاوية حيث يقال قاطع تمام الزاوية هــ .
ويرمز له بالرمز . قتا هـ .
كنسبة مثلثية هو خارج قسمة الوتر على الضلع المقابل في المثلث القائم الزاوية كما في الشكل .
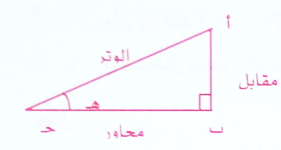
وهكذا : الوتر أ جـ
قتا هـ = ــــــــــــــــــ = ــــــــــــــــــ
المقابل أ ب
وكاقتران مثلثي هو خارج قسمة نصف قطر دائرة الوحدة على الاحداثي الصادي وفي دائرة الوحدة كما في الشكل .
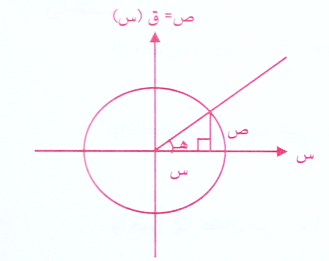
أي ان قتا هـ = 1ص ، ص≠ صفر
ويرتبط باقتران الجيب بالعلاقه التاليه :
قتا هـ=1جاهـ,جاهـ≠صفر
أي ان قتا هـ × جا هـ = 1 دائماً
وقيمته أي عدد حقيقي
أي ان قتا هــ ∊ح الأعداد الحقيقية .
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
