عند مناقشة الذبذبات الصغيرة لبندول بواسطة اعتبارات الطاقة نحصل على صيغة صريحة للزمن الدوري والإزاحة الزاوية θ كدالة في الزمن t. من إعادة فحص سريعة لهذه المسألة يتبين لنا (إذا كانت _maxθ صغيرة) أنها مثال لحركة توافقية بسيطة.

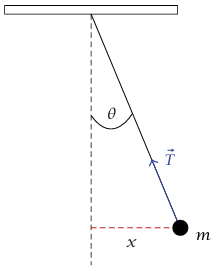
شكل 6–5: بندول ذو سعة ذبذبة صغيرة يخضع لحركة توافقية بسيطة.

إذا كان البندول كتلة نقطية مربوطة في السقف بواسطة وتر طوله L، فإن القوتين الوحيدتين المؤثرتين على m هما قوة شد الوتر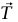 وقوة الجاذبية 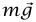. إذا كانت سعة الذبذبة صغيرة، فإن T≃ mg. مركبة  الأفقية هي md²x/dt = –T sin θ باستخدام العلاقة الهندسية L/sin θ = x وT ≃ mg نجد أن:

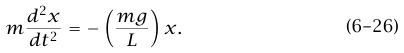
المعادلة (26–6) لها نفس شكل المعادلة (2–6)، مع استبدال mg/L بثابت الزنبرك k؛ وبذلك تكون الحركة الأفقية للبندول ذي الذبذبات الصغيرة هي حركة توافقية بسيطة لها  وزمن دوري 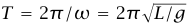 لا يعتمد على السعة (بشرط أن تكون السعة صغيرة). التردد الزاوي ω لا يعتمد على الكتلة؛ لأن «ثابت الزنبرك» يتناسب مع m.

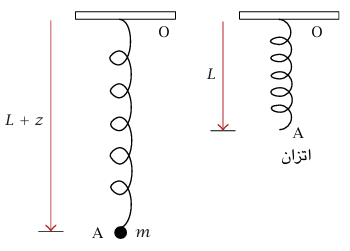
شكل 6–6: جسيم كتلته m معلق على زنبرك رأسي في مثال 6–3.

مثال 6–3 (زنبرك بتذبذب في الاتجاه الرأسي). زنبرك منعدم الكتلة OA له طول اتزان L وثابت زنبرك k. الزنبرك معلق رأسيًّا بحيث تكون 0 مربوطة في السقف وكتلة m مربوطة عند A. أوجد التردد الذي سوف تتذبذب به الكتلة إذا أزيحت عن موضع اتزانها.

الحل. ليكن الطول اللحظي للزنبرك L + z وليكن 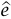 متجه وحدة مشيرًا لأسفل. يؤثر الزنبرك بقوة 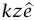– على الكتلة كما أن قوة الجاذبية على الكتلة 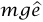. عجلة الكتلة هي  وبالتالي يكون:

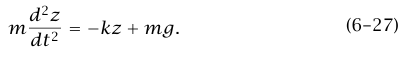
إذا عرفنا u = z – mg/k (لاحظ أن u هي بعد الكتلة عن موضع اتزانها بحيث تناظر قيم u الموجبة النقاط أسفل موضع الاتزان)؛ إذن:

المعادلة (28–6) تصف حركة توافقية بسيطة ترددها الزاوي  وترددها 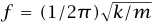؛ وبذلك يكون تأثير الجاذبية هو تغيير موضع الاتزان مع ترك تردد الذبذبات دون تغيير.

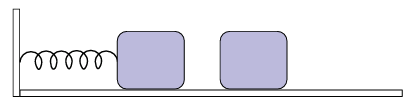
شكل 6–7: كتلة M متصلة بزنبرك وتتصادم مع كتلة مماثلة في مثال 6–4.

مثال 6–4 (كتلة متصلة بزنبرك وتتصادم مع كتلة أخرى). كتلة (M = 0.100kg)، تتحرك على منضدة ملساء مربوطة في نهاية الطرف الأيمن لزنبرك (طول اتزانه m = 1، k = 4.00N/m). الطرف الأيسر للزنبرك مربوط بحائط كان الزنبرك مضغوطًا في البداية بطول مقداره 0.700m ثم تُرك كتلة أخرى (0.100kg أيضًا) موضوعة على المنضدة على مسافة 1m من الحائط عندما تضرب الكتلة المتحركة الكتلة الثابتة تلتصق الكتلتان إحداهما بالأخرى.

(أ) أوجد أقصر مسافة من الحائط للكتلة kg0.200 في حركتها التالية.

(ب) إذا كانت الكتلة الثابتة موضوعة على مسافة 1.200m من الحائط والتصقت الكتلتان إحداهما بالأخرى بعد التصادم، أوجد أقصر مسافة من الحائط لاحقة للكتلة 0.200kg.

(ج) هل تعتمد إجابة (أ) على القيمة العددية للكتلتين (بفرض أن الكتلتين متساويتان) وعلى القيمة العددية لثابت الزنبرك k؟

الحل. (أ) هي الطاقة E للكتلة 0.100kg طاقة جهد صرفة (1/2) kx²_max، عند لحظة الانطلاق. وبما أن التصادم يحدث عند 0 = x، فإن الطاقة تكون حركية صرفة عند هذه النقطة. نستطيع حساب السرعة v للكتلة .0100kg قبل التصادم مباشرة، لكن هذا غير ضروري. مقدار سرعة الكتلة 0.200kg بعد التصادم مباشرة هو 2/v (من حفظ كمية التحرك، لا تكون الطاقة محفوظة أثناء التصادم). طاقة حركة الكتلة 0.200kg بعد التصادم مباشرة هي (1/2) (2M) (v/2)² = (1/4) Mv² = E/2 وبما أن الطاقة الكلية بعد التصادم تساوي نصف الطاقة الكلية قبل التصادم، فإن قيمة x_max بعد التصادم تساوي 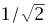 مرة قيمتها قبل التصادم؛ وبذلك بعد التصادم تكون x_max = 0.3/1.414 = 0.212m، وأصغر مسافة من الحائط 1.0 – .212 = 0.212m. واضح أن هذه النتيجة لا تعتمد على القيمة العددية M = 0.100kg أو قيمة k.

(ب) كثيرًا ما يكون من المفيد تعليميًّا حل مسألة ما بدلالة الرموز (التي تمثل الكميات المعطاة، مثل k وM) بدلًا من إدخال قيم عددية سابقة لأوانها. إذا فعلنا ذلك سوف نرى أن إجابة (ب) لا تعتمد على قيمة k أو M. لندع x₀ ترمز لقيمة x عند نقطة إطلاق M = 0.100kg الابتدائية (x₀ = –0.300m) ودع x₁ ترمز إلى قيمة x عند نقطة حدوث التصادم (x₁ = 0.200m). تكون طاقة الكتلة M قبل التصادم هي (1/2) kx²₀. وتكون طاقة حركة الكتلة M قبل التصادم مباشرة:
 .(1/2) kx₀² – (1/2) kx₁² دع X_max ترمز إلى أقصى قيمة لـ x في الحركة بعد التصادم. إذن تكون الطاقة الكلية للكتلة ₂M بعد التصادم (1/2) kX_max² وطاقة حركة الكتلة بعد التصادم مباشرة هي (1/2) kX_max² – (1/2) kX₁². سبق أن وضحنا أنه عندما يصدم جسيم متحرك جسيمًا ثابتًا له نفس كتلته، وتلتصق الكتلتان إحداهما بالأخرى؛ فإن طاقة الحركة بعد التصادم مباشرة تكون مساوية لنصف طاقة الحركة قبل التصادم مباشرة (لا تساهم القوة الخارجية المحدودة (الزنبرك) المؤثرة أثناء زمن تصادم متناهي الصغر بأي كمية حركة في النظام؛ لذا يمكننا استخدام مبدأ حفظ كمية التحرك.) وبذلك نجد أن:

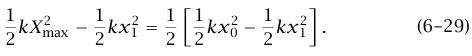
وبحسابات جبرية بسيطة نصل إلى (ج):

وبإدخال الأعداد، نجد أن X_max = 0.255m، وأصغر مسافة من الحائط هي 1.0 – 0.255 = 0.745m لم يستخدم هذا الحل أيا من قيمتي M وk العدديتين.

بالطبع هناك طرق (مكافئة) أخرى لحل الجزأين (أ) و(ب) من هذه المسألة، ستؤدي جميعها إلى المعادلة (30–6). يمكن هنا أن نتعلم درسًا مهما للغاية: حتى قبل حل المسألة، نستطيع أن نعرف أن الإجابة لا تعتمد على الرمزين k أو M. نرى ذلك من اعتبارنا لأبعاد الكميات المدخلة. في النظام المتري، تكون الوحدات الأساسية هي الطول، والكتلة والزمن وحدة القوة (النيوتن) كمية مشتقة أبعادها هي: (الكتلة)×(الطول) / (الزمن)². ثابت الزنبرك K أبعاده هي: (الكتلة) × (الزمن)². والكمية Xmax / xo لا أبعاد لها لكونها نسبة بين طولين. سوف يعطي الحل X_max / x₀ بدلالة الكميات المدخلة x₀, x₁, k, M. الكمية اللابعدية الوحيدة التي تستطيع تكوينها من المدخلات الأربعة هي x₀ / x₁. من المستحيل أن تدخل k أو M في كمية لابعدية (سيكون الموقف مختلفًا إذا كانت المسألة تتضمن ثابتي زنبرك أو كتلتين مختلفتين، وسيكون هناك في أي من هذه الحالات نسب لابعدية إضافية). يمكن لهذا النوع من طريقة التفكير، الذي يطلق عليه التحليل البعدي، أن يكون مفيدًا جدًّا.

مثال 6–5 (زنبركان متصلان). كما هو مبين في شكل 6–8، OA زنبرك له طول اتزان L₁ وثابت زنبركk₁ . O مربوط بالحائط و A مربوط بزنبرك آخر AB له طول اتزان L₂ وثابت زنبرك K₂. ما القوة المطلوبة لبقاء B على مسافة L₁ + L₂ + x  من الحائط؟

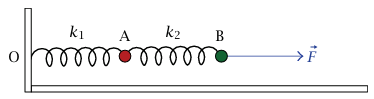
شكل 6–8: زنبركان متصلان تحت تأثير قوة في مثال 6–5.

الحل. ليكن 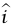 متجه وحدة في اتجاه اليمين. إذا أثرنا بقوة  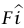على B، فإن B تؤثر بقوة 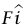– علينا، ولا بد عندئذ أن يكون الطول A هو L₂ + F/k₂. في حالة الاتزان لا بد أن تتلاشى القوة المحصلة على AB؛ وبالتالي لا بد أن تؤثر OA بقوة 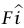– على AB ويكون الطول OA عندئذ هو L₂ + F/k₁؛ وبذلك يكون: