There are not only mechanical examples of oscillating systems but electrical ones as well. Waves are related to oscillating systems, except that wave oscillations appear not only as time-oscillations at one place, but propagate in space as well.

If we have two sources of sound which have slightly different frequencies and if we listen to both at the same time, then sometimes the waves come with the crests together and sometimes with the crest and trough together (see Fig. 47–1). The rising and falling of the sound that results is the phenomenon of beats or, in other words, of interference in time. The second phenomenon involves the wave patterns which result when the waves are confined within a given volume and reflect back and forth from walls.

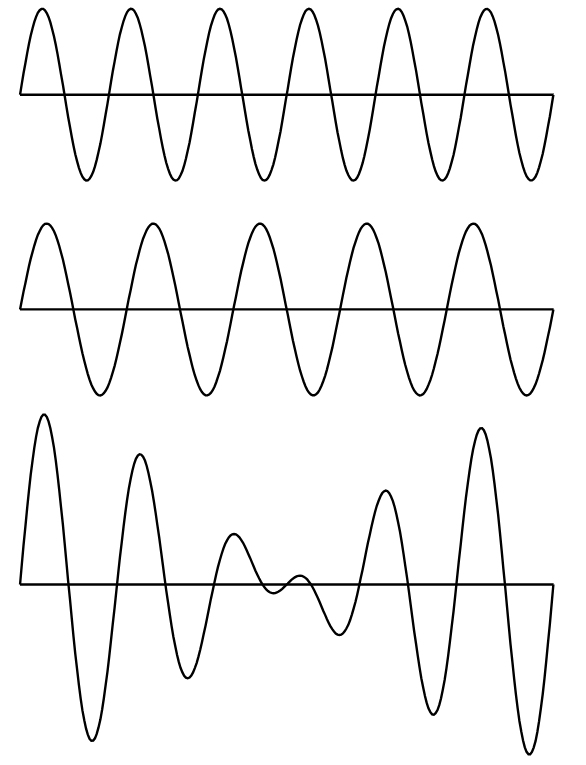
Fig. 47–1. Interference in time of two sound sources with slightly different frequencies, resulting in beats.

These effects could have been discussed, of course, for the case of electromagnetic waves. The reason for not having done this is that by using one example we would not generate the feeling that we are actually learning about many different subjects at the same time. In order to emphasize the general applicability of waves beyond electrodynamics, we consider here a different example, in particular sound waves.

Other examples of waves are water waves consisting of long swells that we see coming in to the shore, or the smaller water waves consisting of surface tension ripples. As another example, there are two kinds of elastic waves in solids; a compressional (or longitudinal) wave in which the particles of the solid oscillate back and forth along the direction of propagation of the wave (sound waves in a gas are of this kind), and a transverse wave in which the particles of the solid oscillate in a direction perpendicular to the direction of propagation. Earthquake waves contain elastic waves of both kinds, generated by a motion at some place in the earth’s crust.

Still another example of waves is found in modern physics. These are waves which give the probability amplitude of finding a particle at a given place—the “matter waves” which we have already discussed. Their frequency is proportional to the energy and their wave number is proportional to the momentum. They are the waves of quantum mechanics.

The speed of light is the same for radiowaves, blue light, green light, or for any other wavelength. Because of this behavior, when we began to describe the wave phenomenon, we did not notice at first that we had wave propagation. Instead, we said that if a charge is moved at one place, the electric field at a distance x was proportional to the acceleration, not at the time t, but at the earlier time t−x/c. Therefore if we were to picture the electric field in space at some instant of time, as in Fig. 47–2, the electric field at a time t later would have moved the distance ct, as indicated in the figure. Mathematically, we can say that in the one-dimensional example we are taking, the electric field is a function of x−ct. We see that at t=0, it is some function of x. If we consider a later time, we need only to increase x somewhat to get the same value of the electric field. For example, if the maximum field occurred at x=3 at time zero, then to find the new position of the maximum field at time t we need

x – ct = 3 or x = 3 + ct.

We see that this kind of function represents the propagation of a wave.

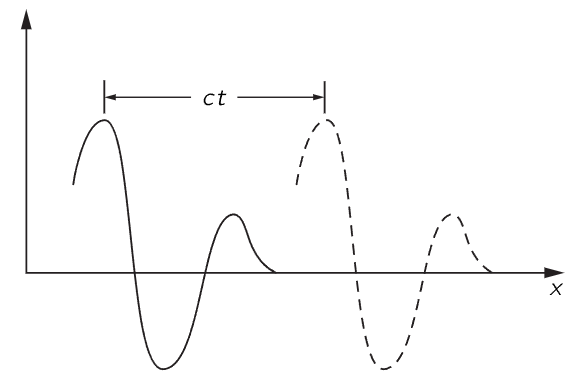
Fig. 47–2. The solid curve shows what the electric field might be like at some instant of time and the dashed curve shows what the electric field is at a time t later.

Such a function, f(x−ct), then represents a wave. We may summarize this description of a wave by saying simply that

f (x − ct) = f (x + Δx – c (t + Δt)),

when Δx = c Δt. There is, of course, another possibility, i.e., that instead of a source to the left as indicated in Fig. 47–2, we have a source on the right, so that the wave propagates toward negative x. Then the wave would be described by g(x+ct).

There is the additional possibility that more than one wave exists in space at the same time, and so the electric field is the sum of the two fields, each one propagating independently. This behavior of electric fields may be described by saying that if f₁(x−ct) is a wave, and if f₂(x−ct) is another wave, then their sum is also a wave. This is called the principle of superposition. The same principle is valid in sound.

We are familiar with the fact that if a sound is produced, we hear with complete fidelity the same sequence of sounds as was generated. If we had high frequencies travelling faster than low frequencies, a short, sharp noise would be heard as a succession of musical sounds. Similarly, if red light travelled faster than blue light, a flash of white light would be seen first as red, then as white, and finally as blue. We are familiar with the fact that this is not the case. Both sound and light travel with a speed in air which is very nearly independent of frequency.

In the case of light (electromagnetic waves) we gave a rule which determined the electric field at a point as a result of the acceleration of a charge. One might expect now that what we should do is give a rule whereby some quality of the air, say the pressure, is determined at a given distance from a source in terms of the source motion, delayed by the travel time of the sound. In the case of light this procedure was acceptable because all that we knew was that a charge at one place exerts a force on another charge at another place. The details of propagation from the one place to the other were not absolutely essential. In the case of sound, however, we know that it propagates through the air between the source and the hearer, and it is certainly a natural question to ask what, at any given moment, the pressure of the air is. We would like, in addition, to know exactly how the air moves. In the case of electricity, we could accept a rule, since we could say that we do not yet know the laws of electricity, but we cannot make the same remark with regard to sound. We would not be satisfied with a rule stating how the sound pressure moves through the air, because the process ought to be understandable as a consequence of the laws of mechanics. In short, sound is a branch of mechanics, and so it is to be understood in terms of Newton’s laws. The propagation of sound from one place to another is merely a consequence of mechanics and the properties of gases, if it propagates in a gas, or of the properties of liquids or solids, if it propagates through such mediums. Later we shall derive the properties of light and its wave propagation in a similar way from the laws of electrodynamics.