Let us consider the reflection of particle waves from a crystal. A crystal is a thick thing which has a whole lot of similar atoms—we will include some complications later—in a nice array. The question is how to set the array so that we get a strong reflected maximum in a given direction for a given beam of, say, light (x-rays), electrons, neutrons, or anything else. In order to obtain a strong reflection, the scattering from all of the atoms must be in phase. There cannot be equal numbers in phase and out of phase, or the waves will cancel out. The way to arrange things is to find the regions of constant phase, as we have already explained; they are planes which make equal angles with the initial and final directions (Fig. 38–4).

Fig. 38–4. Scattering of waves by crystal planes.

If we consider two parallel planes, as in Fig. 38–4, the waves scattered from the two planes will be in phase provided the difference in distance travelled by a wavefront is an integral number of wavelengths. This difference can be seen to be 2dsinθ, where d is the perpendicular distance between the planes. Thus the condition for coherent reflection is

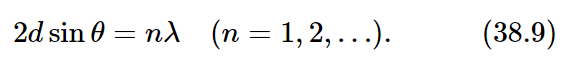
If, for example, the crystal is such that the atoms happen to lie on planes obeying condition (38.9) with n=1, then there will be a strong reflection. If, on the other hand, there are other atoms of the same nature (equal in density) halfway between, then the intermediate planes will also scatter equally strongly and will interfere with the others and produce no effect. So d in (38.9) must refer to adjacent planes; we cannot take a plane five layers farther back and use this formula!

As a matter of interest, actual crystals are not usually as simple as a single kind of atom repeated in a certain way. Instead; if we make a two-dimensional analog, they are much like wallpaper, in which there is some kind of figure which repeats all over the wallpaper. By “figure” we mean, in the case of atoms, some arrangement—calcium and a carbon and three oxygens, etc., for calcium carbonate, and so on—which may involve a relatively large number of atoms. But whatever it is, the figure is repeated in a pattern. This basic figure is called a unit cell.

The basic pattern of repetition defines what we call the lattice type; the lattice type can be immediately determined by looking at the reflections and seeing what their symmetry is. In other words, where we find any reflections at all determines the lattice type, but in order to determine what is in each of the elements of the lattice one must take into account the intensity of the scattering at the various directions. Which directions scatter depends on the type of lattice, but how strongly each scatters is determined by what is inside each unit cell, and in that way the structure of crystals is worked out.

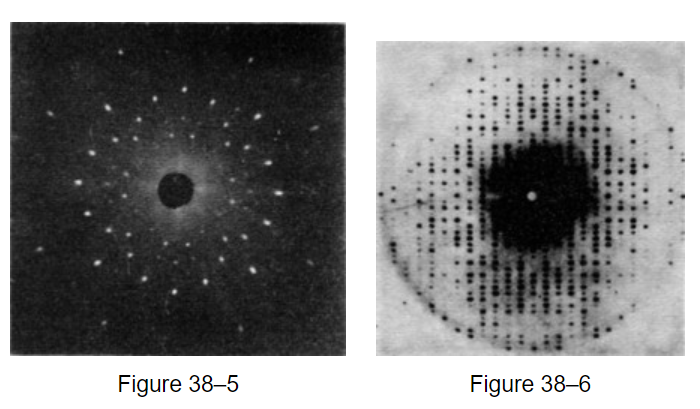
Two photographs of x-ray diffraction patterns are shown in Figs. 38–5 and 38–6; they illustrate scattering from rock salt and myoglobin, respectively.

Incidentally, an interesting thing happens if the spacings of the nearest planes are less than λ/2. In this case (38.9) has no solution for n. Thus if λ is bigger than twice the distance between adjacent planes then there is no side diffraction pattern, and the light—or whatever it is—will go right through the material without bouncing off or getting lost. So in the case of light, where λ is much bigger than the spacing, of course it does go through and there is no pattern of reflection from the planes of the crystal.

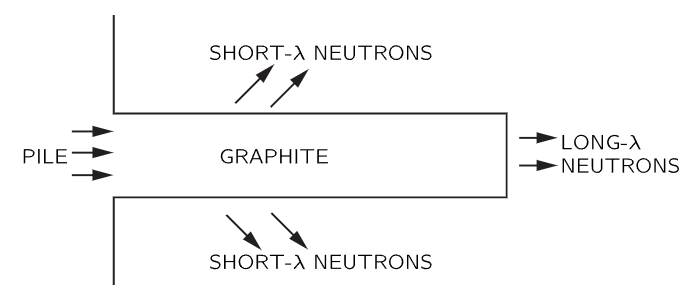
Fig. 38–7. Diffusion of pile neutrons through graphite block.

This fact also has an interesting consequence in the case of piles which make neutrons (these are obviously particles, for anybody’s money!). If we take these neutrons and let them into a long block of graphite, the neutrons diffuse and work their way along (Fig. 38–7). They diffuse because they are bounced by the atoms, but strictly, in the wave theory, they are bounced by the atoms because of diffraction from the crystal planes. It turns out that if we take a very long piece of graphite, the neutrons that come out the far end are all of long wavelength! In fact, if one plots the intensity as a function of wavelength, we get nothing except for wavelengths longer than a certain minimum (Fig. 38–8). In other words, we can get very slow neutrons that way. Only the slowest neutrons come through; they are not diffracted or scattered by the crystal planes of the graphite, but keep going right through like light through glass, and are not scattered out the sides. There are many other demonstrations of the reality of neutron waves and waves of other particles.

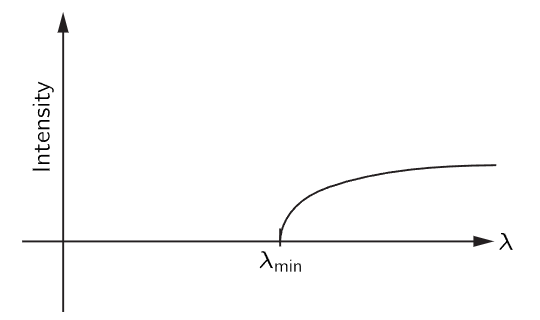
Fig. 38–8. Intensity of neutrons out of graphite rod as function of wavelength.