This is the way Heisenberg stated the uncertainty principle originally: If you make the measurement on any object, and you can determine the x-component of its momentum with an uncertainty Δp, you cannot, at the same time, know its x-position more accurately than Δx≥ℏ/2Δp. The uncertainties in the position and momentum at any instant must have their product greater than or equal to half the reduced Planck constant. This is a special case of the uncertainty principle that was stated above more generally. The more general statement was that one cannot design equipment in any way to determine which of two alternatives is taken, without, at the same time, destroying the pattern of interference.

Let us show for one particular case that the kind of relation given by Heisenberg must be true in order to keep from getting into trouble. We imagine a modification of the experiment of Fig. 37–3, in which the wall with the holes consists of a plate mounted on rollers so that it can move freely up and down (in the x-direction), as shown in Fig. 37–6. By watching the motion of the plate carefully we can try to tell which hole an electron goes through. Imagine what happens when the detector is placed at x=0. We would expect that an electron which passes through hole 1 must be deflected downward by the plate to reach the detector. Since the vertical component of the electron momentum is changed, the plate must recoil with an equal momentum in the opposite direction. The plate will get an upward kick. If the electron goes through the lower hole, the plate should feel a downward kick. It is clear that for every position of the detector, the momentum received by the plate will have a different value for a traversal via hole 1 than for a traversal via hole 2. So! Without disturbing the electrons at all, but just by watching the plate, we can tell which path the electron used.

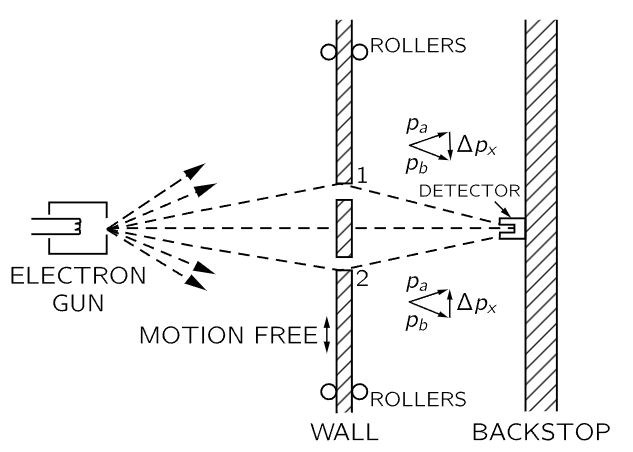
Fig. 37–6. An experiment in which the recoil of the wall is measured.

Now in order to do this it is necessary to know what the momentum of the screen is, before the electron goes through. So when we measure the momentum after the electron goes by, we can figure out how much the plate’s momentum has changed. But remember, according to the uncertainty principle we cannot at the same time know the position of the plate with an arbitrary accuracy. But if we do not know exactly where the plate is we cannot say precisely where the two holes are. They will be in a different place for every electron that goes through. This means that the center of our interference pattern will have a different location for each electron. The wiggles of the interference pattern will be smeared out. We shall show quantitatively in the next chapter that if we determine the momentum of the plate sufficiently accurately to determine from the recoil measurement which hole was used, then the uncertainty in the x-position of the plate will, according to the uncertainty principle, be enough to shift the pattern observed at the detector up and down in the x-direction about the distance from a maximum to its nearest minimum. Such a random shift is just enough to smear out the pattern so that no interference is observed.

The uncertainty principle “protects” quantum mechanics. Heisenberg recognized that if it were possible to measure the momentum and the position simultaneously with a greater accuracy, the quantum mechanics would collapse. So he proposed that it must be impossible. Then people sat down and tried to figure out ways of doing it, and nobody could figure out a way to measure the position and the momentum of anything—a screen, an electron, a billiard ball, anything—with any greater accuracy. Quantum mechanics maintains its perilous but accurate existence.