


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 2024-03-09
التاريخ: 1-1-2017
التاريخ: 2024-03-09
التاريخ: 3-5-2017
|
For our particular system, the differential equation that we have been solving is
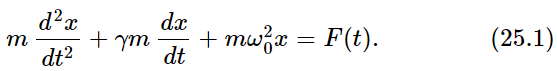
Now this particular combination of “operations” on the variable x has the interesting property that if we substitute (x+y) for x, then we get the sum of the same operations on x and y; or, if we multiply x by a, then we get just a times the same combination. This is easy to prove. Just as a “shorthand” notation, because we get tired of writing down all those letters in (25.1), we shall use the symbol 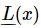 instead. When we see this, it means the left-hand side of (25.1), with x substituted in. With this system of writing,
instead. When we see this, it means the left-hand side of (25.1), with x substituted in. With this system of writing, 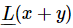 would mean the following:
would mean the following:
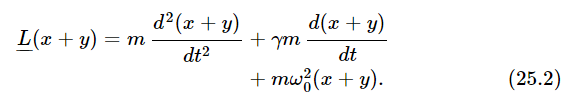
(We underline the  so as to remind ourselves that it is not an ordinary function.) We sometimes call this an operator notation, but it makes no difference what we call it, it is just “shorthand.”
so as to remind ourselves that it is not an ordinary function.) We sometimes call this an operator notation, but it makes no difference what we call it, it is just “shorthand.”
Our first statement was that
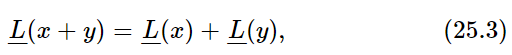
which of course follows from the fact that a(x+y)=ax+ay, d(x+y)/dt=dx/dt+dy/dt, etc.
Our second statement was, for constant a,

[Actually, (25.3) and (25.4) are very closely related, because if we put x+x into (25.3), this is the same as setting a=2 in (25.4), and so on.]
In more complicated problems, there may be more derivatives, and more terms in  ; the question of interest is whether the two equations (25.3) and (25.4) are maintained or not. If they are, we call such a problem a linear problem. In this chapter we shall discuss some of the properties that exist because the system is linear, to appreciate the generality of some of the results that we have obtained in our special analysis of a special equation.
; the question of interest is whether the two equations (25.3) and (25.4) are maintained or not. If they are, we call such a problem a linear problem. In this chapter we shall discuss some of the properties that exist because the system is linear, to appreciate the generality of some of the results that we have obtained in our special analysis of a special equation.
Now let us study some of the properties of linear differential equations, having illustrated them already with the specific equation (25.1) that we have studied so closely. The first property of interest is this: suppose that we have to solve the differential equation for a transient, the free oscillation with no driving force. That is, we want to solve

Suppose that, by some hook or crook, we have found a particular solution, which we shall call x1. That is, we have an x1 for which 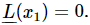 Now we notice that ax1A is also a solution to the same equation; we can multiply this special solution by any constant whatever, and get a new solution. In other words, if we had a motion of a certain “size,” then a motion twice as “big” is again a solution. Proof:
Now we notice that ax1A is also a solution to the same equation; we can multiply this special solution by any constant whatever, and get a new solution. In other words, if we had a motion of a certain “size,” then a motion twice as “big” is again a solution. Proof: 
Next, suppose that, by hook or by crook, we have not only found one solution x1, but also another solution, x2. (Remember that when we substituted x=eiαt for finding the transients, we found two values for α, that is, two solutions, x1 and x2) Now let us show that the combination (x1+x2) is also a solution. In other words, if we put x=x1+x2, x is again a solution of the equation. Why? Because, if  and
and 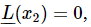 then
then 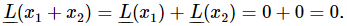 So if we have found a number of solutions for the motion of a linear system, we can add them together.
So if we have found a number of solutions for the motion of a linear system, we can add them together.
Combining these two ideas, we see, of course, that we can also add six of one and two of the other: if x1 is a solution, so is αx1. Therefore, any sum of these two solutions, such as (αx1+βx2), is also a solution. If we happen to be able to find three solutions, then we find that any combination of the three solutions is again a solution, and so on. It turns out that the number of what we call independent solutions1 that we have obtained for our oscillator problem is only two. The number of independent solutions that one finds in the general case depends upon what is called the number of degrees of freedom. We shall not discuss this in detail now, but if we have a second-order differential equation, there are only two independent solutions, and we have found both of them; so, we have the most general solution.
Now let us go on to another proposition, which applies to the situation in which the system is subjected to an outside force. Suppose the equation is

and suppose that we have found a special solution of it. Let us say that Joe’s solution is xJ, and that  Suppose we want to find yet another solution; suppose we add to Joe’s solution one of those that was a solution of the free equation (25.5), say x1. Then we see by (25.3) that
Suppose we want to find yet another solution; suppose we add to Joe’s solution one of those that was a solution of the free equation (25.5), say x1. Then we see by (25.3) that

Therefore, to the “forced” solution we can add any “free” solution, and we still have a solution. The free solution is called a transient solution.
When we have no force acting, and suddenly turn one on, we do not immediately get the steady solution that we solved for with the sine wave solution, but for a while there is a transient which sooner or later dies out, if we wait long enough. The “forced” solution does not die out, since it keeps on being driven by the force. Ultimately, for long periods of time, the solution is unique, but initially the motions are different for different circumstances, depending on how the system was started.
__________________________________________________________________
Margin
1- Solutions which cannot be expressed as linear combinations of each other are called independent.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
ملاكات العتبة العباسية المقدسة تُنهي أعمال غسل حرم مرقد أبي الفضل العباس (عليه السلام) وفرشه
|
|
|