
آخر المواضيع المضافة


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 21-12-2015
التاريخ: 26-10-2015
التاريخ: 29-10-2015
التاريخ: 29-10-2015
|
هو الاقتران الذي تنطبق عليه القاعدة التالية :
ق ( - س) = - ق (س) لكل س∊ح
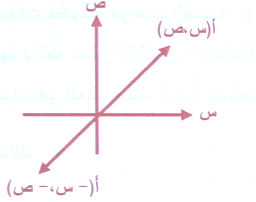
وهذا معناه أن قاعدة الاقتران ق(س) تتغير إشارتها فقط بوضع –س بدلاً من س وتفسير ذلك هندسياً كما في الشكل .
أن منحني الاقتران متماثل لنقطة الأصل والأمثلة عديدة ومنها:
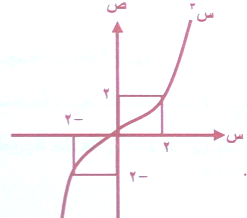
ق(س) = س3
حيث ق( - س) = ( - س)3 = - س3
أي ان ق(2) = 32 = 8
ق( - 2) = ( - 2)3 = - 8
1
وكذلك ق(س) = ـــــــ
س
1 1
حيث ق( - س) = ــــــــــ = ـــ ــــــــ
ــ س س
وكذلك ق( س) = جا س
حيث ق(س) = جا – س = - جا س وهكذا.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|