For over 200 years the equations of motion enunciated by Newton were believed to describe nature correctly, and the first time that an error in these laws was discovered, the way to correct it was also discovered. Both the error and its correction were discovered by Einstein in 1905.

Newton’s Second Law, which we have expressed by the equation

F=d(mv)/dt,

was stated with the tacit assumption that m is a constant, but we now know that this is not true, and that the mass of a body increases with velocity. In Einstein’s corrected formula m has the value

where the “rest mass” m₀ represents the mass of a body that is not moving and c is the speed of light, which is about 3×10⁵ km⋅sec⁻¹ or about 186,000 mi⋅sec⁻¹.

For those who want to learn just enough about it so they can solve problems, that is all there is to the theory of relativity—it just changes Newton’s laws by introducing a correction factor to the mass. From the formula itself it is easy to see that this mass increase is very small in ordinary circumstances. If the velocity is even as great as that of a satellite, which goes around the earth at 5 mi/sec, then v/c=5/186,000: putting this value into the formula shows that the correction to the mass is only one part in two to three billion, which is nearly impossible to observe. Actually, the correctness of the formula has been amply confirmed by the observation of many kinds of particles, moving at speeds ranging up to practically the speed of light. However, because the effect is ordinarily so small, it seems remarkable that it was discovered theoretically before it was discovered experimentally. Empirically, at a sufficiently high velocity, the effect is very large, but it was not discovered that way. Therefore, it is interesting to see how a law that involved so delicate a modification (at the time when it was first discovered) was brought to light by a combination of experiments and physical reasoning. Contributions to the discovery were made by a number of people, the final result of whose work was Einstein’s discovery.

There are really two Einstein theories of relativity. This chapter is concerned with the Special Theory of Relativity, which dates from 1905. In 1915 Einstein published an additional theory, called the General Theory of Relativity. This latter theory deals with the extension of the Special Theory to the case of the law of gravitation; we shall not discuss the General Theory here.

The principle of relativity was first stated by Newton, in one of his corollaries to the laws of motion: “The motions of bodies included in a given space are the same among themselves, whether that space is at rest or moves uniformly forward in a straight line.” This means, for example, that if a space ship is drifting along at a uniform speed, all experiments performed in the space ship and all the phenomena in the space ship will appear the same as if the ship were not moving, provided, of course, that one does not look outside. That is the meaning of the principle of relativity. This is a simple enough idea, and the only question is whether it is true that in all experiments performed inside a moving system the laws of physics will appear the same as they would if the system were standing still. Let us first investigate whether Newton’s laws appear the same in the moving system.

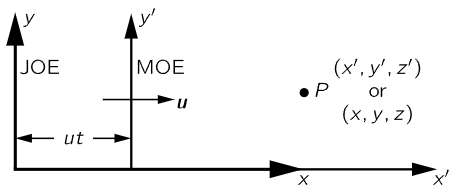
Fig. 15–1. Two coordinate systems in uniform relative motion along their x–axes.

Suppose that Moe is moving in the x–direction with a uniform velocity u, and he measures the position of a certain point, shown in Fig. 15–1. He designates the “x–distance” of the point in his coordinate system as x′. Joe is at rest, and measures the position of the same point, designating its x–coordinate in his system as x. The relationship of the coordinates in the two systems is clear from the diagram. After time t Moe’s origin has moved a distance ut, and if the two systems originally coincided,

If we substitute this transformation of coordinates into Newton’s laws, we find that these laws transform to the same laws in the primed system; that is, the laws of Newton are of the same form in a moving system as in a stationary system, and therefore it is impossible to tell, by making mechanical experiments, whether the system is moving or not.

The principle of relativity has been used in mechanics for a long time. It was employed by various people, in particular Huygens, to obtain the rules for the collision of billiard balls, in much the same way as we used it in Chapter 10 to discuss the conservation of momentum. In the 19th century interest in it was heightened as the result of investigations into the phenomena of electricity, magnetism, and light. A long series of careful studies of these phenomena by many people culminated in Maxwell’s equations of the electromagnetic field, which describe electricity, magnetism, and light in one uniform system. However, the Maxwell equations did not seem to obey the principle of relativity. That is, if we transform Maxwell’s equations by the substitution of equations (15.2), their form does not remain the same; therefore, in a moving space ship the electrical and optical phenomena should be different from those in a stationary ship. Thus one could use these optical phenomena to determine the speed of the ship; in particular, one could determine the absolute speed of the ship by making suitable optical or electrical measurements. One of the consequences of Maxwell’s equations is that if there is a disturbance in the field such that light is generated, these electromagnetic waves go out in all directions equally and at the same speed c, or 186,000 mi/sec. Another consequence of the equations is that if the source of the disturbance is moving, the light emitted goes through space at the same speed c. This is analogous to the case of sound, the speed of sound waves being likewise independent of the motion of the source.

This independence of the motion of the source, in the case of light, brings up an interesting problem:

Suppose we are riding in a car that is going at a speed u, and light from the rear is going past the car with speed c. Differentiating the first equation in (15.2) gives

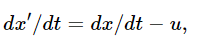
which means that according to the Galilean transformation the apparent speed of the passing light, as we measure it in the car, should not be c but should be c−u. For instance, if the car is going 100,000 mi/sec, and the light is going 186,000 mi/sec, then apparently the light going past the car should go 86,000 mi/sec. In any case, by measuring the speed of the light going past the car (if the Galilean transformation is correct for light), one could determine the speed of the car. A number of experiments based on this general idea were performed to determine the velocity of the earth, but they all failed—they gave no velocity at all. We shall discuss one of these experiments in detail, to show exactly what was done and what was the matter; something was the matter, of course, something was wrong with the equations of physics. What could it be?