


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 19-10-2015
Date: 20-10-2015
Date: 19-10-2015
|
Born: about 280 BC in Greece
Died: about 210 BC
 We know nothing of Nicomedes' life. To make a guess at dating his life we have some limits which are given by references to his work. Nicomedes himself criticised the method that Eratosthenes used to duplicate the cube and we have made a reasonably accurate guess at Eratosthenes's life span (276 BC - 194 BC). A less certain piece of information comes from Apollonius choosing to name a curve 'sister of the conchoid' which is assumed to be a name he has chosen to compliment Nicomedes' discovery of the conchoid. Since Apollonius lived from about 262 BC to 190 BC these two pieces of information give a fairly accurate estimate of Nicomedes' dates. However, as we remarked the second of these pieces of information cannot be relied on but nevertheless, from what we know of the mathematics of Nicomedes, the deduced dates are fairly convincing.
We know nothing of Nicomedes' life. To make a guess at dating his life we have some limits which are given by references to his work. Nicomedes himself criticised the method that Eratosthenes used to duplicate the cube and we have made a reasonably accurate guess at Eratosthenes's life span (276 BC - 194 BC). A less certain piece of information comes from Apollonius choosing to name a curve 'sister of the conchoid' which is assumed to be a name he has chosen to compliment Nicomedes' discovery of the conchoid. Since Apollonius lived from about 262 BC to 190 BC these two pieces of information give a fairly accurate estimate of Nicomedes' dates. However, as we remarked the second of these pieces of information cannot be relied on but nevertheless, from what we know of the mathematics of Nicomedes, the deduced dates are fairly convincing.
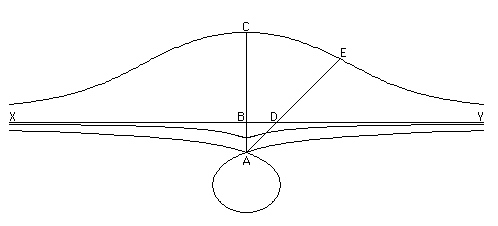 Nicomedes is famous for his treatise On conchoid lines which contain his discovery of the curve known as the conchoid of Nicomedes. How did Nicomedes define the curve. Consider the diagram. We are given a line XY and a point A not on the line. ABC is drawn perpendicular to XY cutting it at B and having the length BC some fixed value, say b. Then rotate ABC about A so that, in an arbitrary position ADE then DE = b. So if a point P on the conchoid is joined to A then PA cuts the line XY in a point at distance b from P.
Nicomedes is famous for his treatise On conchoid lines which contain his discovery of the curve known as the conchoid of Nicomedes. How did Nicomedes define the curve. Consider the diagram. We are given a line XY and a point A not on the line. ABC is drawn perpendicular to XY cutting it at B and having the length BC some fixed value, say b. Then rotate ABC about A so that, in an arbitrary position ADE then DE = b. So if a point P on the conchoid is joined to A then PA cuts the line XY in a point at distance b from P.
Nicomedes recognised three distinct forms in this family but the sources do not go into detail on this point. It is believed that they must be the three branches of the curve. The conchoid can be used in solving both the problems of trisection of an angle and of the duplication of a cube. Both these problems were solved by Nicomedes using the conchoid, in fact as Toomer writes in [1]:-
As far as is known, all applications of the conchoid made in antiquity were developed by Nicomedes himself. It was not until the late sixteenth century, when the works of Pappus and Eutocius describing the curve became generally known, that interest in it revived...
As indicated in this quote Pappus also wrote about Nicomedes, in particular he wrote about his solution to the problem of trisecting an angle (see for example [2]):-
Nicomedes trisected any rectilinear angle by means of the conchoidal curves, the construction, order and properties of which he handed down, being himself the discoverer of their peculiar character.
Nicomedes also used the quadratrix, discovered by Hippias, to solve the problem of squaring the circle. Pappus tells us (see for example [2]):-
For the squaring of the circle there was used by Dinostratus, Nicomedes and certain other later persons a certain curve which took its name from this property, for it is called by them square-forming
in other words the quadratrix.
Eutocius tells us that Nicomedes [2]:-
... prided himself inordinately on his discovery of this curve, contrasting it with Eratosthenes's mechanism for finding any number of mean proportionals, to which he objected formally and at length on the ground that it was impracticable and entirely outside the spirit of geometry.
Books:
1.T L Heath, A History of Greek Mathematics (2 Vols.) (Oxford, 1921).
Articles:



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|