


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
أقرأ أيضاً
التاريخ: 26-1-2022
التاريخ: 27-1-2022
التاريخ: 29-1-2022
التاريخ: 27-1-2022
|
صياغة مسائل البرمجة الخطيةProblem Formulation
مقدمة
يهتم هذا المقال بصياغة مسائل البرمجة الخطية والتي تعني تحويل المشاكل الحقيقية إلى مسائل رياضية من خلال خطوات يحسب فيها شكل النموذج الرياضي ومستوى المتغيرات، نوع المتغيرات، وحدود المشكلة ومركباتها وذلك من خلال الأمثلة التالية:
مثال 1:
تنتج شركة إنتاجية ثلاثة منتجات. وكل منتج يحتاج إلى ثلاثة أنواع من المدخلات هي: : المادة الخام، الطاقة البشرية، والطاقة الميكانيكية، ويوضح الجدول رقم (1-1) احتياجات وحدة المنتج من مدخلات الإنتاج والإنتاجية لكل مدخل والربح المتوقع لكل منها:
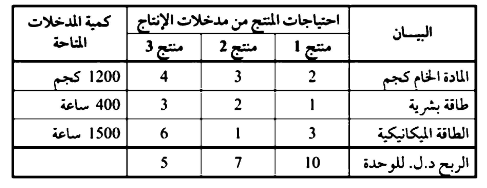
جدول (1-1)
المطلوب:
صياغة نموذج البرمجة الخطية لتحديد الكمية الواجب إنتاجها من كل منتج لتعظيم لربح إلى أقصى حد ممكن.
الحل:
1- تحديد متغيرات النموذج (Determination of the decision variables):
باعتبار أن المطلوب كمية كل منتج يسعى إلى تعظيم الربح، عليه فإن المتغيرات هي:
X1 كمية الإنتاج من المنتج 1
X2 كمية الإنتاج من المنتج 2
X3 كمية الإنتاج من المنتج 3
2- تحديد دالة الهدف (Formulation of the objective function)
باعتبار أن الهدف من تحديد كمية الإنتاج من كل منتج هو تعظيم الربح الإجمالي من كل المنتوجات التي تنتجها الشركة، عليه فإن دالة الهدف وفقاً للمعلومات الموضحة في الجدول (1-3):
Maximize Z= 10x1 + 7x2 + 5x3 تعظیم
3- تحديد القيود (Determination of the constraints):
تتمثل القيود المفروضة على الإنتاج في التحكم في كمية المواد الخام والطاقة البشرية والطاقة الميكانيكية، ولتحقيق هذه القيود يجب أن لا تحدث أي زيادة في الطلب على هذه المدخلات لتعظيم كمية الإنتاج من المنتوجات الثلاثة وبالتالي يمكن صياغة القيود على النحو الآتي:




|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|