المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Equivalence Relation |
 1387
 05:13 مساءً
date: 11-1-2022 |
Author : Skiena, S 
Book or Source : Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley 
Page and Part : ...|
Read More
Date: 14-2-2017
2099
Date: 29-12-2021
1273
Date: 9-1-2022
1436
|
An equivalence relation on a set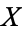 
is a subset of 
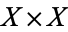, i.e., a collection 
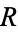of ordered pairs of elements of 
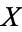, satisfying certain properties. Write "
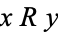" to mean 
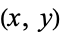is an element of 
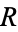, and we say "
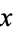is related to 
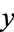," then the properties are
1. Reflexive: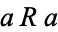 
for all 
,
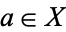2. Symmetric: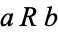 
implies 
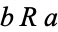for all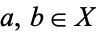 
3. Transitive: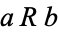 
and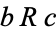 
imply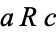 
for all 
,
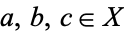where these three properties are completely independent. Other notations are often used to indicate a relation, e.g.,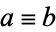 
or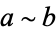 
.
REFERENCES:
Skiena, S. Implementing Discrete Mathematics: Combinatorics and Graph Theory with Mathematica. Reading, MA: Addison-Wesley, p. 18, 1990.
Stewart, I. and Tall, D. The Foundations of Mathematics. Oxford, England: Oxford University Press, 1977.
|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
العتبة العباسية المقدسة تستعد لإطلاق الحفل المركزي لتخرج طلبة الجامعات العراقية
|
|
|
