


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-1-2022
Date: 13-1-2022
Date: 26-12-2021
|
Let 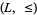 be any complete lattice. Suppose
be any complete lattice. Suppose 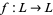 is monotone increasing (or isotone), i.e., for all
is monotone increasing (or isotone), i.e., for all 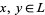 ,
, 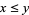 implies
implies 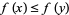 . Then the set of all fixed points of
. Then the set of all fixed points of  is a complete lattice with respect to
is a complete lattice with respect to  (Tarski 1955)
(Tarski 1955)
Consequently,  has a greatest fixed point
has a greatest fixed point 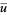 and a least fixed point
and a least fixed point 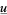 . Moreover, for all
. Moreover, for all 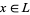 ,
, 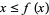 implies
implies 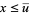 , whereas
, whereas 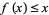 implies
implies 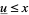 .
.
Consider three examples:
1. Let 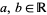 satisfy
satisfy 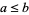 , where
, where 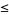 is the usual order of real numbers. Since the closed interval
is the usual order of real numbers. Since the closed interval ![[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline19.gif) is a complete lattice, every monotone increasing map
is a complete lattice, every monotone increasing map ![f:[a,b]->[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline20.gif) has a greatest fixed point and a least fixed point. Note that
has a greatest fixed point and a least fixed point. Note that 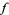 need not be continuous here.
need not be continuous here.
2. For 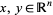 declare
declare 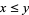 to mean that
to mean that 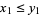 ,
,  ,
, 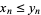 (coordinatewise order). Let
(coordinatewise order). Let 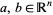 satisfy
satisfy 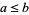 . Then the set
. Then the set
![[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline29.gif) |
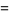 |
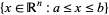 |
(1) |
 |
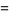 |
![[a_1,b_1]×...×[a_n,b_n]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline34.gif) |
(2) |
is a complete lattice (with respect to the coordinatewise order). Hence every monotone increasing map ![f:[a,b]->[a,b]](https://mathworld.wolfram.com/images/equations/TarskisFixedPointTheorem/Inline35.gif) has a greatest fixed point and a least fixed point.
has a greatest fixed point and a least fixed point.
3. Let 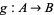 and
and 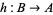 be injections. Then there is a bijection
be injections. Then there is a bijection 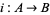 (Schröder-Bernstein theorem), which can be constructed as follows. The power set of
(Schröder-Bernstein theorem), which can be constructed as follows. The power set of 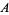 ordered by set inclusion,
ordered by set inclusion, 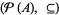 , is a complete lattice. Since the map
, is a complete lattice. Since the map 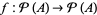 ,
,
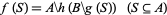 |
(3) |
is monotone increasing, it has a fixed point 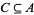 . As
. As 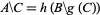 , a bijection
, a bijection 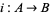 can be defined just by setting
can be defined just by setting
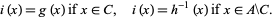 |
(4) |
REFERENCES:
Tarski, A. "A Lattice-Theoretical Fixpoint Theorem and Its Applications." Pacific J. Math. 5, 285-309, 1955.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|