


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 12-1-2022
Date: 29-12-2021
Date: 2-1-2022
|
If 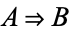 and
and 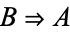 (i.e.,
(i.e., 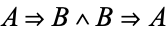 , where
, where 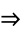 denotes implies), then
denotes implies), then 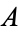 and
and 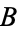 are said to be equivalent, a relationship which is written symbolically in this work as
are said to be equivalent, a relationship which is written symbolically in this work as 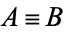 . The following table summarizes some notations in common use.
. The following table summarizes some notations in common use.
| symbol | references |
 |
Moore (1910, p. 150), Whitehead and Russell (1910, pp. 5-38), Carnap (1958, p. 8), Curry (1977, p. 35), Itô (1986, p. 147), Gellert et al. 1989 (p. 333), Cajori (1993, pp. 303 and 307), Church (1996, p. 78), Harris and Stocker (1998, p. 471) |
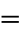 |
Wittgenstein (1922, pp. 46-47), Cajori (1993, p. 313) |
 |
Mendelson (1997, p. 13), Råde and Westergren 2004 (p. 9) |
 |
Harris and Stocker (1998, back flap), DIN 1302 (1999) |
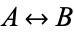 |
Gellert et al. 1989 (p. 333), Harris and Stocker (1998, p. 471), Råde and Westergren 2004 (p. 9) |
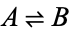 |
Equivalence is implemented in the Wolfram Language as Equal[A, B, ...]. Binary equivalence has the following truth table (Carnap 1958, p. 10), and is the same as 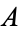 XNOR
XNOR 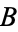 , and
, and 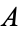 iff
iff 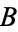 .
.
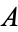 |
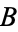 |
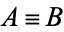 |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Similarly, ternary equivalence has the following truth table.
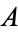 |
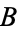 |
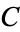 |
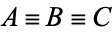 |
| T | T | T | T |
| T | T | F | F |
| T | F | T | F |
| T | F | F | F |
| F | T | T | F |
| F | T | F | F |
| F | F | T | F |
| F | F | F | T |
The opposite of being equivalent is being nonequivalent.
Note that the symbol  is confusingly used in at least two other different contexts. If
is confusingly used in at least two other different contexts. If 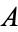 and
and 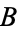 are "equivalent by definition" (i.e.,
are "equivalent by definition" (i.e., 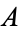 is defined to be
is defined to be 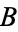 ), this is written
), this is written 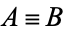 , and "
, and "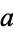 is congruent to
is congruent to 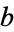 modulo
modulo 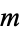 " is written
" is written 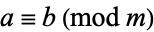 .
.
REFERENCES:
Cajori, F. A History of Mathematical Notations, Vol. 2. New York: Dover, p. 303, 1993.
Carnap, R. Introduction to Symbolic Logic and Its Applications. New York: Dover, p. 8, 1958.
Church, A. Introduction to Mathematical Logic, Vol. 1. Princeton, NJ: Princeton University Press, 1996.
Curry, H. B. Foundations of Mathematical Logic. New York: Dover, 1977.
Deutsches Institut für Normung E. V. DIN 1302: "General Mathematical Symbols and Concepts." Dec. 1, 1999.
Gellert, W.; Gottwald, S.; Hellwich, M.; Kästner, H.; and Künstner, H. (Eds.). VNR Concise Encyclopedia of Mathematics, 2nd ed. New York: Van Nostrand Reinhold, 1989.
Harris, J. W. and Stocker, H. Handbook of Mathematics and Computational Science. New York: Springer-Verlag, 1998.
Itô, K. (Ed.). Encyclopedic Dictionary of Mathematics, 2nd ed., Vol. 1. Cambridge, MA: MIT Press, 1986.
Mendelson, E. Introduction to Mathematical Logic, 4th ed. London: Chapman & Hall, 1997.
Moore, E. H. Introduction to a Form of General Analysis. New Haven, CT: New Haven Math. Colloq., 1910.
Råde, L. and Westergren, B. Mathematics Handbook for Science and Engineering. Berlin: Springer, 2004.
Whitehead, A. N. and Russell, B. Principia Mathematica, Vol. 1. New York: Cambridge University Press, 1910.
Wittgenstein, L. Tractatus Logico-Philosophicus. London, 1922.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|