


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 2-2-2016
Date: 12-1-2022
Date: 16-1-2022
|
A complemented lattice is an algebraic structure 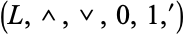 such that
such that 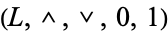 is a bounded lattice and for each element
is a bounded lattice and for each element 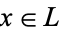 , the element
, the element 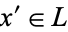 is a complement of
is a complement of 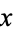 , meaning that it satisfies
, meaning that it satisfies
1. 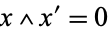
2. 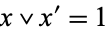 .
.
A related notion is that of a lattice with complements. Such a structure is a bounded lattice 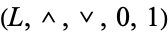 such that for each
such that for each 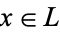 , there is
, there is 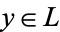 such that
such that 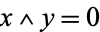 and
and 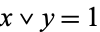 .
.
One difference between these notions is that the class of complemented lattices forms a variety, whilst the class of lattices with complements does not. (The class of lattices with complements is a subclass of the variety of lattices, but it is not a subvariety of the class of lattices.) Every lattice with complements is a reduct of a complemented lattice, by the axiom of choice. To see this, let 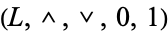 be a lattice with complements. For each
be a lattice with complements. For each 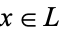 , let
, let 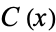 denote the set of complements of
denote the set of complements of 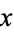 . Because
. Because 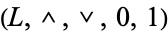 is a lattice with complements, for each
is a lattice with complements, for each 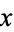 ,
,  is nonempty, so by the axiom of choice, we may choose from each collection
is nonempty, so by the axiom of choice, we may choose from each collection  a distinguished complement
a distinguished complement 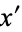 for
for 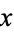 . This defines a function
. This defines a function 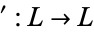 which is a complementation operation, meaning that it satisfies the properties stated above for the complementation operation of a complemented lattice. Augmenting the bounded lattice
which is a complementation operation, meaning that it satisfies the properties stated above for the complementation operation of a complemented lattice. Augmenting the bounded lattice 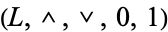 with this operation yields a complemented lattice,
with this operation yields a complemented lattice, 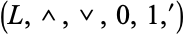 of which the original lattice with complements
of which the original lattice with complements 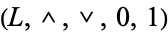 is a reduct.
is a reduct.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|