


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 16-1-2022
Date: 4-1-2022
Date: 17-1-2022
|
The term "natural number" refers either to a member of the set of positive integers 1, 2, 3, ... (OEIS A000027) or to the set of nonnegative integers 0, 1, 2, 3, ... (OEIS A001477; e.g., Bourbaki 1968, Halmos 1974). Regrettably, there seems to be no general agreement about whether to include 0 in the set of natural numbers. In fact, Ribenboim (1996) states "Let  be a set of natural numbers; whenever convenient, it may be assumed that
be a set of natural numbers; whenever convenient, it may be assumed that  ."
."
The set of natural numbers (whichever definition is adopted) is denoted N.
Due to lack of standard terminology, the following terms and notations are recommended in preference to "counting number," "natural number," and "whole number."
| set | name | symbol |
..., 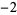 , , 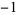 , 0, 1, 2, ... , 0, 1, 2, ... |
integers | Z |
| 1, 2, 3, 4, ... | positive integers | Z-+ |
| 0, 1, 2, 3, 4, ... | nonnegative integers | Z-* |
0, 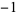 , , 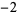 , , 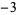 , , 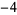 , ... , ... |
nonpositive integers | |
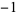 , , 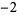 , , 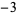 , , 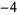 , ... , ... |
negative integers | Z-- |
REFERENCES:
Bourbaki, N. Elements of Mathematics: Theory of Sets. Paris, France: Hermann, 1968.
Courant, R. and Robbins, H. "The Natural Numbers." Ch. 1 in What Is Mathematics?: An Elementary Approach to Ideas and Methods, 2nd ed. Oxford, England: Oxford University Press, pp. 1-20, 1996.
Halmos, P. R. Naive Set Theory. New York: Springer-Verlag, 1974.
Ribenboim, P. "Catalan's Conjecture." Amer. Math. Monthly 103, 529-538, 1996.
Sloane, N. J. A. Sequences A000027/M0472 and A001477 in "The On-Line Encyclopedia of Integer Sequences."
Welbourne, E. "The Natural Numbers." http://www.chaos.org.uk/~eddy/math/found/natural.html.



|
|
|
|
دخلت غرفة فنسيت ماذا تريد من داخلها.. خبير يفسر الحالة
|
|
|
|
|
|
|
ثورة طبية.. ابتكار أصغر جهاز لتنظيم ضربات القلب في العالم
|
|
|
|
|
|
|
سماحة السيد الصافي يؤكد ضرورة تعريف المجتمعات بأهمية مبادئ أهل البيت (عليهم السلام) في إيجاد حلول للمشاكل الاجتماعية
|
|
|