Invariant Manifold

An invariant set 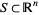 is said to be a  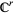(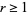) invariant manifold if  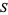has the structure of a  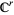differentiable manifold (Wiggins 1990, p. 14).

When stable and unstable invariant manifolds intersect, they do so in a hyperbolic fixed point (saddle point). The invariant manifolds are then called separatrices. A hyperbolic fixed point is characterized by two ingoing stable manifolds and two outgoing unstable manifolds. In integrable systems, incoming 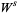 and outgoing  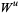manifolds join up smoothly.

REFERENCES:

Rasband, S. N. "Invariant Manifolds." §5.2 in Chaotic Dynamics of Nonlinear Systems. New York: Wiley, pp. 89-92, 1990.

Wiggins, S. "Invariant Manifolds: Linear and Nonlinear Systems." §1.1C in Introduction to Applied Nonlinear Dynamical Systems and Chaos. New York: Springer-Verlag, pp. 14-25, 1990.