Compound Interest

Let 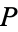 be the principal (initial investment),  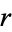be the annual compounded rate,  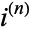the "nominal rate,"  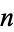be the number of times interest is compounded per year (i.e., the year is divided into  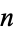conversion periods), and  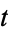be the number of years (the "term"). The interest rate per conversion period is then

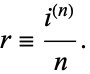(1)

If interest is compounded 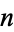 times at an annual rate of  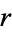(where, for example, 10% corresponds to 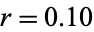), then the effective rate over  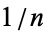the time (what an investor would earn if he did not redeposit his interest after each compounding) is

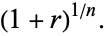(2)

The total amount of holdings 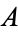 after a time  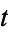when interest is re-invested is then

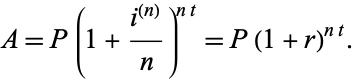(3)

Note that even if interest is compounded continuously, the return is still finite since

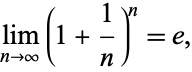(4)

where e is the base of the natural logarithm.

The time required for a given principal to double (assuming 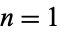 conversion period) is given by solving

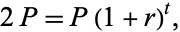(5)

or

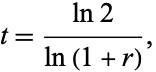(6)

where ln is the natural logarithm. This function can be approximated by the so-called rule of 72:

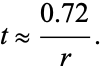(7)

REFERENCES:

Kellison, S. G. The Theory of Interest, 2nd ed. Burr Ridge, IL: Richard D. Irwin, pp. 14-16, 1991.

Milanfar, P. "A Persian Folk Method of Figuring Interest." Math. Mag. 69, 376, 1996.