Kähler Metric

A Kähler metric is a Riemannian metric 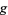 on a complex manifold which gives  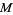a Kähler structure, i.e., it is a Kähler manifold with a Kähler form. However, the term "Kähler metric" can also refer to the corresponding Hermitian metric 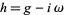, where  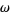is the Kähler form, defined by 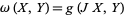. Here, the operator  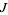is the almost complex structure, a linear map on tangent vectors satisfying 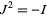, induced by multiplication by 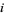. In coordinates 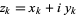, the operator  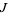satisfies  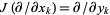and .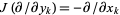

The operator 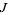 depends on the complex structure, and on a Kähler manifold, it must preserve the Kähler metric. For a metric to be Kähler, one additional condition must also be satisfied, namely that it can be expressed in terms of the metric and the complex structure. Near any point 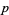, there exists holomorphic coordinates  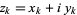such that the metric has the form

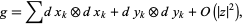where 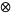 denotes the vector space tensor product; that is, it vanishes up to order two at 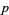. Hence, any geometric equation in  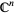involving only the first derivatives can be defined on a Kähler manifold. Note that a generic metric can be written to vanish up to order two, but not necessarily in holomorphic coordinates, using a Gaussian coordinate system.