


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-6-2021
Date: 5-7-2021
Date: 28-6-2017
|
The set of fixed points which do not move as a knot is transformed into itself is not a knot. The conjecture was proved in 1978 (Morgan and Bass 1984). According to Morgan and Bass (1984), the Smith conjecture stands in the first rank of mathematical problems when measured by the amount and depth of new mathematics required to solve it.
The generalized Smith conjecture considers 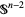 to be a piecewise linear
to be a piecewise linear 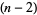 -dimensional hypersphere in
-dimensional hypersphere in 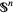 , and
, and 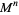 the
the 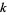 -fold cyclic covering of
-fold cyclic covering of 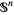 branched along
branched along 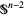 , and asks if
, and asks if 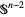 is unknotted if
is unknotted if 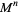 is an
is an 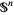 (Hartley 1983). This conjecture is true for
(Hartley 1983). This conjecture is true for 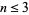 , and false for
, and false for 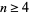 , with counterexamples in the latter case provided by Giffen (1966), Gordon (1974), and Sumners (1975).
, with counterexamples in the latter case provided by Giffen (1966), Gordon (1974), and Sumners (1975).
REFERENCES:
Giffen, C. H. "The Generalized Smith Conjecture." Amer. J. Math. 88, 187-198, 1966.
Gordon, C. M. "On the Higher-Dimensional Smith Conjecture." Proc. London Math. Soc. 29, 98-110, 1974.
Hartley, R. "Whitehead Torsion and the Smith Conjecture." Michigan Math. J. 30, 121-128, 1983.
Morgan, J. W. and Bass, H. (Eds.). The Smith Conjecture, Papers Presented at the Symposium Held at Columbia University, New York, 1979. Orlando, FL: Academic Press, 1984.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, pp. 350-351, 1976.
Smith, P. A. "Transformations of Finite Period. II." Ann. Math. 40, 690-711, 1939.
Summers, D. W. "Smooth 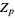 Actions on Spheres which Leave Knots Pointwise Fixed." Trans. Amer. Math. Soc. 205, 193-203, 1975.
Actions on Spheres which Leave Knots Pointwise Fixed." Trans. Amer. Math. Soc. 205, 193-203, 1975.
Waldhausen, F. "Über Involutionen der 3-Sphäre." Topology 8, 81-91, 1969.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|