المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Habiro Move |
 1925
 03:53 مساءً
date: 16-6-2021 |
Author : Habiro, K. 
Book or Source : "Claspers and Finite Type Invariants of Links." Geom. Topol. 4 
Page and Part : ...|
Read More
Date: 14-8-2021
2239
Date: 10-6-2021
1571
Date: 4-7-2021
1430
|
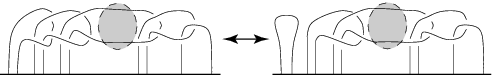
A knot move illustrated above. Two knots cannot be distinguished using Vassiliev invariants of order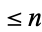 
iff they are related by a sequence of such moves (Habiro 2000). There is a correspondence between the Habiro move and solution of the baguenaudier puzzle (Przytycki and Sikora 2000).
REFERENCES:
Habiro, K. "Claspers and Finite Type Invariants of Links." Geom. Topol. 4, 1-83, 2000.
Przytycki, J. H. and Sikora, A. S. "Topological Insights from the Chinese Rings." 21 Jul 2000. https://arxiv.org/abs/math.GT/0007134.
|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|
