Writhe

A knot property, also called the twist number, defined as the sum of crossings  of a link ,

(1)

where  defined to be  if the overpass slants from top left to bottom right or bottom left to top right and  is the set of crossings of an oriented link.

The writhe of a minimal knot diagram is not a knot invariant, as exemplified by the Perko pair, which have differing writhes (Hoste et al. 1998). This is because while the writhe is invariant under Reidemeister moves II and III, it may increase or decrease by one for a Reidemeister move of type I (Adams 1994, p. 153).

Thistlethwaite (1988) proved that if the writhe of a reduced alternating projection of a knot is not 0, then the knot is not amphichiral (Adams 1994).

A formula for the writhe is given by

(2)

where  is parameterized by  for  along the length of the knot by parameter , and the frame  associated with  is

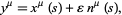(3)

where 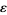 is a small parameter,  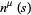is a unit vector field normal to the curve at 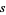, and the vector field  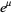is given by

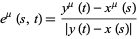(4)

(Kaul 1999).

Letting Lk be the linking number of the two components of a ribbon, Tw be the twist, and Wr be the writhe, then the Calugareanu theorem states that

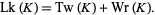(5)

(Adams 1994, p. 187).

REFERENCES:

Adams, C. C. The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots. New York: W. H. Freeman, pp. 152-153 and 185, 1994.

Hoste, J.; Thistlethwaite, M.; and Weeks, J. "The First 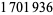 Knots." Math. Intell. 20, 33-48, Fall 1998.

Kauffman, L. Knots and Physics. Teaneck, NJ: World Scientific, p. 19, 1991.

Kaul, R. K. "Topological Quantum Field Theories--A Meeting Ground for Physicists and Mathematicians." 15 Jul 1999. https://arxiv.org/abs/hep-th/9907119.

Thistlethwaite, M. B. "Kauffman's Polynomial and Alternating Links.' Topology 27, 311-318, 1988.