المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Conway Polynomial |
 1626
 06:08 مساءً
date: 12-6-2021 |
Author : Doll, H. and Hoste, J. 
Book or Source : "A Tabulation of Oriented Links." Math. Comput. 57 
Page and Part : ...|
Read More
Date: 28-7-2021
1479
Date: 28-6-2017
1683
Date: 10-8-2021
1792
|
The Conway polynomial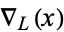 
, sometimes known as the Conway-Alexander polynomial, is a modified version of the Alexander polynomial 
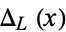that was formulated by J. H. Conway (Livingston 1993, pp. 207-215). It is a reparametrization of the Alexander polynomial given by
 |
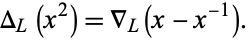The skein relationship convention used by for the Conway polynomial is
 |
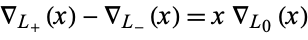(Doll and Hoste 1991).
Examples of Alexander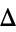 
and Conway 
polynomials for common knots are given in the following table
knot  |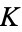
 |
 |
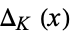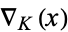| trefoil knot |  |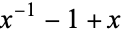
 |
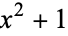| figure eight knot |  |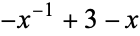
 |
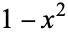| Solomon's seal knot |  |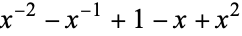
 |
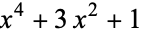| stevedore's knot |  |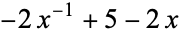
 |
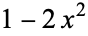| Miller Institute knot |  |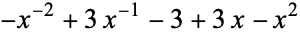
 |
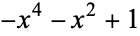REFERENCES:
Doll, H. and Hoste, J. "A Tabulation of Oriented Links." Math. Comput. 57, 747-761, 1991.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., 1993.
|
|
|
|
تفوقت في الاختبار على الجميع.. فاكهة "خارقة" في عالم التغذية
|
|
|
|
|
|
|
أمين عام أوبك: النفط الخام والغاز الطبيعي "هبة من الله"
|
|
|
|
|
|
|
قسم شؤون المعارف ينظم دورة عن آليات عمل الفهارس الفنية للموسوعات والكتب لملاكاته
|
|
|
