


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 6-6-2021
Date: 2-8-2021
Date: 23-7-2021
|
 |
 |
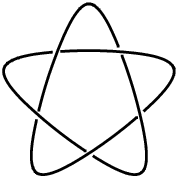
Solomon's seal knot is the prime (5,2)-torus knot 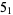 with braid word
with braid word 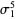 . It is also known as the cinquefoil knot (a name derived from certain herbs and shrubs of the rose family which have five-lobed leaves and five-petaled flowers) or the double overhand knot. It has Arf invariant 1 and is not amphichiral, although it is invertible.
. It is also known as the cinquefoil knot (a name derived from certain herbs and shrubs of the rose family which have five-lobed leaves and five-petaled flowers) or the double overhand knot. It has Arf invariant 1 and is not amphichiral, although it is invertible.
The knot group of Solomon's seal knot is
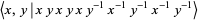 |
(1) |
(Livingston 1993, p. 127).
The Alexander polynomial 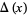 , BLM/Ho polynomial
, BLM/Ho polynomial 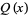 , Conway polynomial
, Conway polynomial 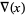 , HOMFLY polynomial
, HOMFLY polynomial 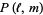 , Jones polynomial
, Jones polynomial 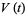 , and Kauffman polynomial F
, and Kauffman polynomial F 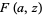 of the Solomon's seal knot are
of the Solomon's seal knot are
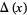 |
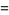 |
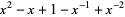 |
(2) |
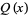 |
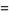 |
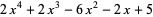 |
(3) |
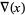 |
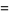 |
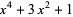 |
(4) |
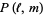 |
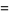 |
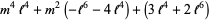 |
(5) |
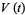 |
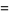 |
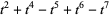 |
(6) |
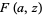 |
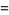 |
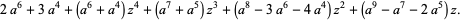 |
(7) |
Surprisingly, the knot 10-132 shares the same Alexander polynomial and Jones polynomial with the Solomon's seal knot. However, no knots on 10 or fewer crossings share the same BLM/Ho polynomial with it.
REFERENCES:
Bar-Natan, D. "The Knot 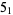 ." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/5.1.html.
." https://www.math.toronto.edu/~drorbn/KAtlas/Knots/5.1.html.
KnotPlot. "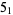 ." https://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=5&id=1.
." https://newweb.cecm.sfu.ca/cgi-bin/KnotPlot/KnotServer/kserver?ncomp=1&ncross=5&id=1.
Livingston, C. Knot Theory. Washington, DC: Math. Assoc. Amer., 1993.
Rolfsen, D. Knots and Links. Wilmington, DE: Publish or Perish Press, p. 53, 1976.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|