


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-9-2016
Date: 28-9-2016
Date: 16-6-2021
|
Let 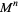 be a compact
be a compact 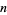 -dimensional oriented Riemannian manifold without boundary, let
-dimensional oriented Riemannian manifold without boundary, let 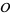 be a group representation of
be a group representation of 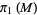 by orthogonal matrices, and let
by orthogonal matrices, and let 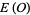 be the associated vector bundle. Suppose further that the Laplacian
be the associated vector bundle. Suppose further that the Laplacian 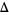 is strictly negative on
is strictly negative on 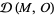 where
where 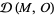 is the linear space of
is the linear space of 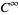 differential k-forms on
differential k-forms on 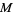 with values in
with values in 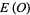 . In this context, the analytic torsion
. In this context, the analytic torsion 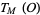 is defined as the positive real root of
is defined as the positive real root of
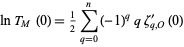 |
where the 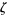 -function is defined by
-function is defined by
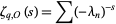 |
for 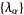 the collection of eigenvalues of
the collection of eigenvalues of 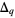 , the restriction of
, the restriction of 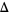 to the collection
to the collection 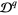 of
of 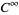 bundle sections of the sheaf
bundle sections of the sheaf 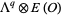 .
.
Intrinsic to the above computation is that 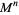 is a real manifold. However, there is a collection of literature on analytic torsion for complex manifolds, the construction of which is nearly identical to the construction given above. Analytic torsion on complex manifolds is sometimes called del bar torsion.
is a real manifold. However, there is a collection of literature on analytic torsion for complex manifolds, the construction of which is nearly identical to the construction given above. Analytic torsion on complex manifolds is sometimes called del bar torsion.
REFERENCES:
Ray, D. B. and Singer, I. M. "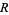 -Torsion and the Laplacian on Riemannian Manifolds." Adv. Math. 7, 145-210, 1971.
-Torsion and the Laplacian on Riemannian Manifolds." Adv. Math. 7, 145-210, 1971.
Ray, D. B. and Singer, I. M. "Analytic Torsion for Complex Manifolds." Ann. Math., Second Series, 98, 154-177, 1973.



|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
جامعة سومر: حفل تخرج طلبة الجامعات يسهم بتنمية الروح الوطنية ويشجع على المثابرة والاجتهاد
|
|
|