


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-4-2021
Date: 23-3-2021
Date: 4-5-2021
|
A sufficient condition on the Lindeberg-Feller central limit theorem. Given random variates 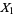 ,
, 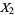 , ..., let
, ..., let 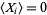 , the variance
, the variance 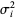 of
of 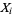 be finite, and variance of the distribution consisting of a sum of
be finite, and variance of the distribution consisting of a sum of 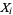 s
s
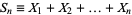 |
(1) |
be
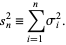 |
(2) |
In the terminology of Zabell (1995), let
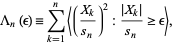 |
(3) |
where 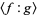 denotes the expectation value of
denotes the expectation value of 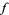 restricted to outcomes
restricted to outcomes 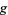 , then the Lindeberg condition is
, then the Lindeberg condition is
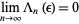 |
(4) |
for all 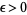 (Zabell 1995).
(Zabell 1995).
In the terminology of Feller (1971), the Lindeberg condition assumed that for each 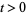 ,
,
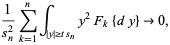 |
(5) |
or equivalently
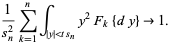 |
(6) |
Then the distribution
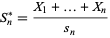 |
(7) |
tends to the normal distribution with zero expectation and unit variance (Feller 1971, p. 256). The Lindeberg condition (5) guarantees that the individual variances 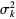 are small compared to their sum
are small compared to their sum 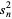 in the sense that for given
in the sense that for given 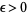 for all sufficiently large
for all sufficiently large 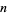 ,
, 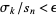 for
for 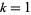 , ...,
, ..., 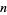 (Feller 1971, p. 256).
(Feller 1971, p. 256).
REFERENCES:
Feller, W. "Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung." Math. Zeit. 40, 521-559, 1935.
Feller, W. "Über den zentralen Grenzwertsatz der Wahrscheinlichkeitsrechnung, II." Math. Zeit. 42, 301-312, 1935.
Feller, W. An Introduction to Probability Theory and Its Applications, Vol. 2, 3rd ed. New York: Wiley, pp. 257-258, 1971.
Lindeberg, J. W. "Eine neue Herleitung des Exponential-gesetzes in der Wahrscheinlichkeitsrechnung." Math. Zeit. 15, 211-235, 1922.
Trotter, H. F. "An Elementary Proof of the Central Limit Theorem." Arch. Math. 10, 226-234, 1959.
Wallace, D. L. "Asymptotic Approximations to Distributions." Ann. Math. Stat. 29, 635-654, 1958.
Zabell, S. L. "Alan Turing and the Central Limit Theorem." Amer. Math. Monthly 102, 483-494, 1995.



|
|
|
|
علامات بسيطة في جسدك قد تنذر بمرض "قاتل"
|
|
|
|
|
|
|
أول صور ثلاثية الأبعاد للغدة الزعترية البشرية
|
|
|
|
|
|
|
مكتبة أمّ البنين النسويّة تصدر العدد 212 من مجلّة رياض الزهراء (عليها السلام)
|
|
|