


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 18-4-2021
Date: 23-4-2021
Date: 13-2-2021
|
Amazingly, the distribution of a sum of two normally distributed independent variates 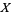 and
and 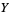 with means and variances
with means and variances 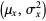 and
and 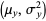 , respectively is another normal distribution
, respectively is another normal distribution
![P_(X+Y)(u)=1/(sqrt(2pi(sigma_x^2+sigma_y^2)))e^(-[u-(mu_x+mu_y)]^2/[2(sigma_x^2+sigma_y^2)]),](https://mathworld.wolfram.com/images/equations/NormalSumDistribution/NumberedEquation1.gif) |
(1) |
which has mean
 |
(2) |
and variance
 |
(3) |
By induction, analogous results hold for the sum of 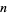 normally distributed variates.
normally distributed variates.
An alternate derivation proceeds by noting that
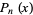 |
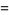 |
![F_t^(-1){[phi(t)]^n}(x)](https://mathworld.wolfram.com/images/equations/NormalSumDistribution/Inline8.gif) |
(4) |
 |
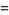 |
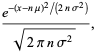 |
(5) |
where 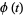 is the characteristic function and
is the characteristic function and ](https://mathworld.wolfram.com/images/equations/NormalSumDistribution/Inline13.gif) is the inverse Fourier transform, taken with parameters
is the inverse Fourier transform, taken with parameters 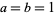 .
.
More generally, if  is normally distributed with mean
is normally distributed with mean 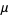 and variance
and variance 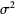 , then a linear function of
, then a linear function of  ,
,
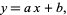 |
(6) |
is also normally distributed. The new distribution has mean 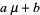 and variance
and variance 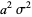 , as can be derived using the moment-generating function
, as can be derived using the moment-generating function
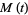 |
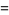 |
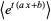 |
(7) |
 |
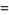 |
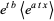 |
(8) |
 |
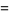 |
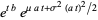 |
(9) |
 |
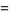 |
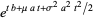 |
(10) |
 |
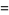 |
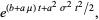 |
(11) |
which is of the standard form with
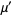 |
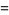 |
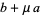 |
(12) |
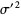 |
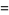 |
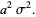 |
(13) |
For a weighted sum of independent variables
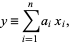 |
(14) |
the expectation is given by
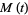 |
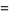 |
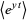 |
(15) |
 |
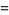 |
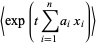 |
(16) |
 |
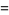 |
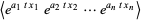 |
(17) |
 |
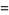 |
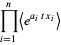 |
(18) |
 |
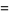 |
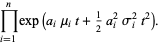 |
(19) |
Setting this equal to
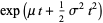 |
(20) |
gives
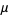 |
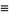 |
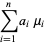 |
(21) |
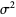 |
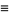 |
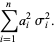 |
(22) |
Therefore, the mean and variance of the weighted sums of 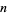 random variables are their weighted sums.
random variables are their weighted sums.
If 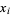 are independent and normally distributed with mean 0 and variance
are independent and normally distributed with mean 0 and variance 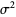 , define
, define
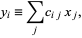 |
(23) |
where 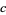 obeys the orthogonality condition
obeys the orthogonality condition
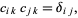 |
(24) |
with 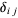 the Kronecker delta. Then
the Kronecker delta. Then 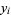 are also independent and normally distributed with mean 0 and variance
are also independent and normally distributed with mean 0 and variance 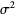 .
.
Cramer showed the converse of this result in 1936, namely that if 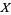 and
and 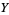 are independent variates and
are independent variates and 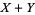 has a normal distribution, then both
has a normal distribution, then both 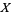 and
and 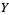 must be normal. This result is known as Cramer's theorem.
must be normal. This result is known as Cramer's theorem.



|
|
|
|
علامات تحذيرية قد تسبق الموت القلبي المفاجئ لدى الشباب
|
|
|
|
|
|
|
استنساخ ذئاب عملاقة وشرسة "انقرضت منذ آلاف السنين"
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|