


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 26-2-2021
Date: 11-3-2021
Date: 30-4-2021
|
A point process 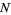 on
on 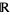 is said to be interval stationary if for every
is said to be interval stationary if for every 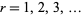 and for all integers
and for all integers 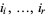 , the joint distribution of
, the joint distribution of
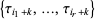 |
does not depend on 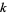 ,
, 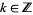 . Here,
. Here, 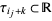 is an interval for all
is an interval for all 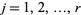 .
.
As pointed out in a variety of literature (e.g., Daley and Vere-Jones 2002, pp 45-46), the notion of an interval stationary point process is intimately connected to (though fundamentally different from) the idea of a stationary point process in the Borel set sense of the term. Worth noting, too, is the difference between interval stationarity and other notions such as simple/crude stationarity.
Though it has been done, it is more difficult to extend to 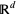 the notion of interval stationarity; doing so requires a significant amount of additional machinery and reflects, overall, the significantly-increased structural complexity of higher-dimensional Euclidean spaces (Daley and Vere-Jones 2007).
the notion of interval stationarity; doing so requires a significant amount of additional machinery and reflects, overall, the significantly-increased structural complexity of higher-dimensional Euclidean spaces (Daley and Vere-Jones 2007).
REFERENCES:
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume I: Elementary Theory and Methods, 2nd ed. New York: Springer, 2003.
Daley, D. J. and Vere-Jones, D. An Introduction to the Theory of Point Processes Volume II: General Theory and Structure, 2nd ed. New York: Springer, 2007.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|