المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Excess |
 1387
 01:49 صباحاً
date: 20-2-2021 |
Author : Biggs, N. L. and Ito, T. 
Book or Source : "Graphs with Even Girth and Small Excess." Math. Proc. Cambridge Philos. Soc. 88 
Page and Part : ...|
Read More
Date: 14-3-2021
2823
Date: 26-4-2021
2373
Date: 14-4-2021
1640
|
The kurtosis excess of a distribution is sometimes called the excess, or excess coefficient.
In graph theory, excess refers to the quantity
 |
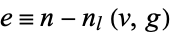(1) |
for a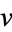 
-regular graph 
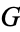on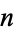 
nodes with girth 
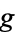, where
 |
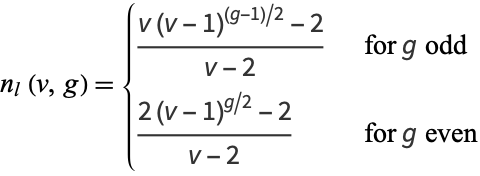(2) |
(Biggs and Ito 1980, Wong 1982). A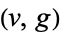 
-cage graph having 
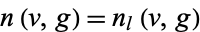vertices (i.e., the minimal number, so that the excess is 
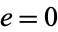) is called a Moore graph.
REFERENCES:
Biggs, N. L. and Ito, T. "Graphs with Even Girth and Small Excess." Math. Proc. Cambridge Philos. Soc. 88, 1-10, 1980.
Wong, P. K. "Cages--A Survey." J. Graph Th. 6, 1-22, 1982.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
مركز الكفيل يباشر بتنفيذ الأعمال الطباعية الخاصّة بحفل تخرّج طلبة الجامعات العراقية
|
|
|
