


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 22-4-2020
Date: 3-11-2019
Date: 20-9-2020
|
An Euler-Jacobi pseudoprime to a base 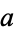 is an odd composite number
is an odd composite number 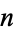 such that
such that 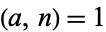 and the Jacobi symbol
and the Jacobi symbol 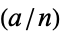 satisfies
satisfies
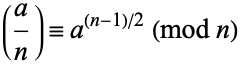 |
(Guy 1994; but note that Guy calls these simply "Euler pseudoprimes"). No odd composite number is an Euler-Jacobi pseudoprime for all bases 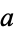 relatively prime to it. This class includes some Carmichael numbers, all strong pseudoprimes to base
relatively prime to it. This class includes some Carmichael numbers, all strong pseudoprimes to base 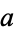 , and all Euler pseudoprimes to base
, and all Euler pseudoprimes to base 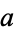 . An Euler pseudoprime is pseudoprime to at most 1/2 of all possible bases less than itself.
. An Euler pseudoprime is pseudoprime to at most 1/2 of all possible bases less than itself.
The first few base-2 Euler-Jacobi pseudoprimes are 561, 1105, 1729, 1905, 2047, 2465, ... (OEIS A047713), and the first few base-3 Euler-Jacobi pseudoprimes are 121, 703, 1729, 1891, 2821, 3281, 7381, ... (OEIS A048950). The number of base-2 Euler-Jacobi primes less than 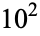 ,
, 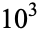 , ... are 0, 1, 12, 36, 114, ... (OEIS A055551).
, ... are 0, 1, 12, 36, 114, ... (OEIS A055551).
REFERENCES:
Guy, R. K. "Pseudoprimes. Euler Pseudoprimes. Strong Pseudoprimes." §A12 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, pp. 27-30, 1994.
Pinch, R. G. E. "The Pseudoprimes Up to 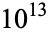 ." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
." ftp://ftp.dpmms.cam.ac.uk/pub/PSP/.
Riesel, H. Prime Numbers and Computer Methods for Factorization, 2nd ed. Boston, MA: Birkhäuser, 1994.
Sloane, N. J. A. Sequences A047713/M5461, A048950, and A055551 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
المجمع العلمي يقيم ورشة تطويرية ودورة قرآنية في النجف والديوانية
|
|
|