5 - 1 - 2 - 9 - 3 أسلوب خط الاتجاه المعدل بالعوامل الموسمية

Seasonal Adjusted Trend Line Method

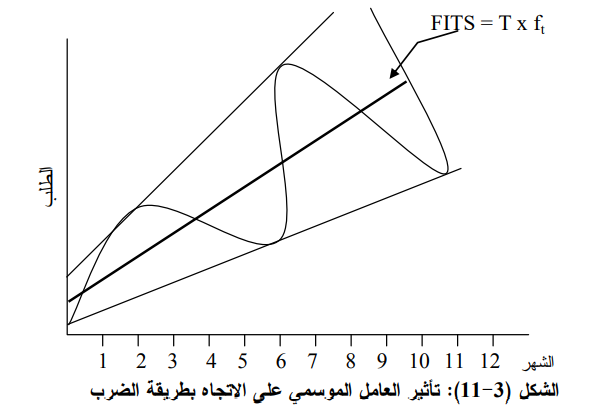
إن الطلب على عدد غير قليل من المنتجات يتأثر بالعوامل الموسمية في أثناء السنة. فالطلب على المرطبات يزداد في أثناء الصيف وينخفض في موسم الشتاء، والطلب على النفط الأبيض لأغراض التدفئة يرتفع في موسم الشتاء وينخفض في موسم الصيف. لذلك ومن اجل الحصول على تنبؤ دقيق ينبغي معرفة قيمة العامل الموسمي (Seasonal Factor) ومن ثم تعديل التنبؤ الذي نحصل عليه بأسلوب خط الاتجاه، بالعامل الموسمي. ولو سلمنا بان الطلب على منتج ما يتأثر بالعوامل الموسمية فهناك سؤال مهم يطرح نفسه إلا وهو: كيف يؤثر العامل الموسمي في الاتجاه؟ وفي الواقع توجد طريقتان لذلك، فاما إن يؤثر العامل الموسمي في الاتجاه بنسبة ثابتة تُضاف إلى الاتجاه بغض النظر عن قيمة الاتجاه، ونُطلق على هذا النوع من التغيرات الموسمية تسمية تعديل الاتجاه بالمتغيرات الموسمية بطريقة الاضافة                    ( Additive Seasonal Variations) واما ان يؤثر العامل الموسمي في الاتجاه بنسبة متغيرة أي قيمة العامل الموسمي تُضرب بقيمة الاتجاه. ونُطلق على النوع من التغيرات الموسمية تسمية تعديل الاتجاه بالمتغيرات الموسمية بطريقة الضرب (Multiplicative Seasonal Variations).   

وتُكتب الصيغة العامة للتنبؤ المعدل في حالة إضافة العامل الموسمي للاتجاه كما يلي :

                         (16-3)FITS = T +f_t             ……….. 

أما الصيغة العامة للتنبؤ في حالة ضرب الاتجاه في العامل الموسمي فإنها تكتب كما يلي:

                        3-17))  …..…….            f_t FITS =T x

FITS = التنبؤ الذي يضم الاتجاه و العامل الموسمی

(Forcast Including Trend & Seasonal Factor)

T = الأتجاه أو التنبؤ الذي نحصل عليه بمعادلة (3-9) وهي:   Y = a + bx

f_t= العامل الموسمي (Seasonal Factor)

والمثال التالي يوضح كيفية تطبيق هذا الأسلوب :

مثال (3-6) 

قرر أحد منتجي أقمشة الحرير الصناعي استخدام أسلوب خط الاتجاه لتنبؤ الطلب على الحرير الصناعي خلال عام 2011. من خلال الخبرة الماضية فان هذا المنتج يعلم بأن الطلب على الحرير الصناعي يتغير حسب فصول السنة وكما يظهر في الجدول (103). والمطلوب تنبؤ الطلب للفصول الأربعة لعام 2011 بأسلوب خط الاتجاه المعدل بالعوامل الموسمية، مرة بطريقة الضرب ومرة بطريقة الإضافة.

الحل :

1.بحساب قيمة ثوابت معادلة الاتجاه العام (a) و (b)، فإن معادلة خط الاتجاه (9-3) هي :

Y = 302 + 56X                                                    

2.وباستخدام المعادلة السابقة نتمكن من إجراء تنبؤ الفصول الأربعة من عام 2011 والتي سيكون ترتيبها في السلسلة x هو 13 و 14 و 15 و 16 للفصول الأول والثاني والثالث والرابع من عام 2011 على التوالي.

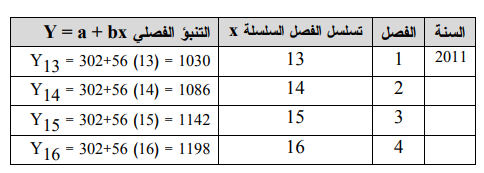
لاحظ أن التنبؤ الفصلي غير معدل بالعوامل الموسمية لذلك ينبغي حساب العوامل الموسمية لكل فصل وكما يلي:

3.حساب العوامل الموسمية

يُحسب العامل الموسمي لكل فصل لبيانات الطلب لعام 2008 والتي تظهر في الجدول (3ــ10) وباتباع الخطوات الاتية :

أ ـ يُحسب الوسط الحسابي للطلب السنوي D بقسمة مجموع الطلب السنوي على عدد فصول السنة ، أي :

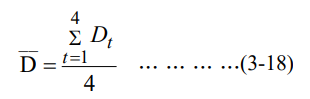
   لان D_t = الطلب الفصلي الحقيقي 

 وبالتعويض فإن الوسط الحسابي للطلب السنوي لعام 2008 هو :

ب ـ يُحسب العامل الموسمي لكل فصل F_t وذلك بقسمة الطلب الحقيقي D_t في كل فصل على متوسط الطلب السنوي وكما في القاعدة الآتية :

 وبإعادة نفس الخطوات على السنتين الأخرتين يمكن الحصول على النتائج التالية :

ج.حساب متوسط العامل الموسمي SF_t لكل فصل وذلك بجمع العوامل الموسمية f_t لكل فصل وقسمة المجموع على عدد السنوات (وهي ثلاث في هذا المثال) 

ولإجراء ذلك نطبق القاعدة التالية :

حيث ان t _t,n  = العامل الموسمي للفصل t  من السنة n .

وبتطبيق القاعدة السابقة نحصل على العامل الموسمي للفصول الاربعة لعام 2011 وكما يلي :

وبنفس الطريقة تم الحصول على العوامل الموسمية للفصول الأخيرة وكما يظهر في نتائج التحليل السابقة .

4. يعدل التنبؤ بالعوامل الموسمية السابقة بطريقة الضرب، أي ضرب العامل الموسي بنتائج التنبؤ من الخطوة (2)، أما بطريقة الاضافة فيتم اضافة مقدار ثابت تحدده الإدارة الى نتائج التنبؤ الموسمي على افتراض أن النمط الموسمی ثابت بغض النظر عن معدل الطلب، وليكن هذا المقدار 50، وعلى هذا الأساس فأن نتائج التنبؤ المعدل بالطريقتين (الضرب والأضافة) تكون كما يلي؛

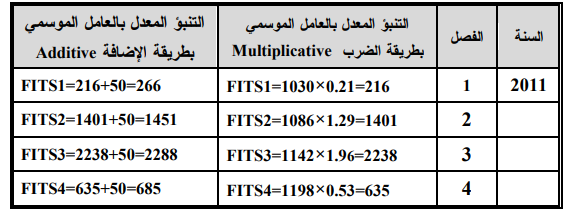
 والآن أي الطريقتين افضل؟ تعديل الاتجاه بطريقة الضرب أم بطريقة الجمع؟ إن الإجابات على هذا السؤال تتطلب معرفة مقدار خطأ التنبؤ (Forecast Error) الذي ينتج عن كل طريقة. وسوف نتناول هذا الموضوع في مبحث لاحق من هذا الفصل.