

المحاسبة

تطور الفكر المحاسبي

الافصاح والقوائم المالية

الرقابة والنظام المحاسبي

نظرية ومعايير المحاسبة الدولية

نظام التكاليف و التحليل المحاسبي

نظام المعلومات و القرارات الادارية

مواضيع عامة في المحاسبة

مفاهيم ومبادئ المحاسبة


ادارة الاعمال


الادارة

الادارة: المفهوم والاهمية والاهداف والمبادئ

وظائف المدير ومنظمات الاعمال

الادارة وعلاقتها بالعلوم الاخرى

النظريات الادارية والفكر الاداري الحديث

التطور التاريخي والمدارس والمداخل الادارية


وظيفة التخطيط

انواع التخطيط

خطوات التخطيط ومعوقاته

مفهوم التخطيط واهميته


وظيفة التنظيم

العملية التنظيمية والهيكل التنظيمي

مفهوم التنظيم و مبادئه


وظيفة التوجيه

الاتصالات

انواع القيادة و نظرياتها

مفهوم التوجيه واهميته


وظيفة الرقابة

انواع الرقابة

خصائص الرقابة و خطواتها

مفهوم الرقابة و اهميتها

اتخاذ القرارات الادارية لحل المشاكل والتحديات

مواضيع عامة في الادارة

المؤسسات الصغيرة والمتوسطة


ادارة الانتاج

ادارة الانتاج: المفهوم و الاهمية و الاهداف و العمليات

التطور التاريخي والتكنلوجي للانتاج

نظام الانتاج وانواعه وخصائصه

التنبؤ والتخطيط و تحسين الانتاج والعمليات

ترتيب المصنع و التخزين والمناولة والرقابة

الموارد البشرية والامداد والتوريد

المالية والمشتريات والتسويق

قياس تكاليف وكفاءة العمل والاداء والانتاج

مواضيع عامة في ادارة الانتاج


ادارة الجودة

الجودة الشاملة: المفهوم و الاهمية و الاهداف و المبادئ

نظام الايزو ومعايير الجودة

ابعاد الجودة و متطلباتها

التطور التاريخي للجودة و مداخلها

الخدمة والتحسين المستمر للجودة

خطوات ومراحل تطبيق الجودة الشاملة

التميز التنافسي و عناصر الجودة

مواضيع عامة في ادارة الجودة


الادارة الاستراتيجية

الادارة الاستراتيجية: المفهوم و الاهمية و الاهداف والمبادئ

اساليب التخطيط الاستراتيجي ومراحله

التطور التاريخي للادارة الاستراتيجية

النظريات و الانظمة و القرارات و العمليات

تحليل البيئة و الرقابة و القياس

الصياغة و التطبيق و التنفيذ والمستويات

مواضيع عامة في الادارة الاستراتيجية


ادارة التسويق

ادارة التسويق : المفهوم و الاهمية و الاهداف و الانواع

استراتيجية التسويق والمزيج التسويقي

البيئة التسويقية وبحوث التسويق

المستهلك والخدمة والمؤسسات الخدمية

الاسواق و خصائص التسويق و انظمته

مواضيع عامة في ادارة التسويق


ادارة الموارد البشرية

ادارة الموارد البشرية : المفهوم و الاهمية و الاهداف و المبادئ

التطور التاريخي لادارة الموارد البشرية

استراتيجية ادارة الموارد البشرية

الوظائف والتعيينات

الحوافز والاجور

التدريب و التنمية

السياسات و التخطيط

التحديات والعولمة ونظام المعلومات

مواضيع عامة في ادارة الموارد البشرية

نظم المعلومات


علوم مالية و مصرفية


المالية العامة

الموازنات المالية

النفقات العامة

الايرادات العامة

مفهوم المالية

التدقيق والرقابة المالية

السياسات و الاسواق المالية

الادارة المالية والتحليل المالي

المؤسسات المالية والمصرفية وادارتها


الاقتصاد

مفهوم ونشأت وعلاقة علم الاقتصاد بالعلوم الاخرى

السياسة الاقتصادية والمالية والنقدية

التحليل الأقتصادي و النظريات

التكتلات والنمو والتنمية الأقتصادية

الاستثمار ودراسة الجدوى الأقتصادية

ألانظمة الاقتصادية

مواضيع عامة في علم الاقتصاد


الأحصاء

تطور علم الاحصاء و علاقته بالعلوم الاخرى

مفهوم واهمية علم الاحصاء

البيانات الأحصائية
أسلوب خط الاتجاه Trend Line Method
المؤلف:
د . عبد الكريم محسن د . صباح مجيد النجار
المصدر:
ادارة الانتاج والعمليات
الجزء والصفحة:
ص112-115
6-1-2021
6955
4 - 1 - 2 - 9 - 3 أسلوب خط الاتجاه Trend Line Method
يعد هذا الأسلوب من الأساليب الشائعة الاستخدام في تنبؤ الطلب على المنتجات. وتفترض هذه الطريقة إن الطلب على المنتجات يتغير (يزيد أو ينقص ) بمرور الزمن، وان ما حدث للطلب في الماضي يمكن ان يتكرر في المستقبل. وتستخدم معادلة خط الاتجاه العام لتقدير الطلب في المستقبل. ويعبر عن هذه المعادلة بالصيغة الأتية :

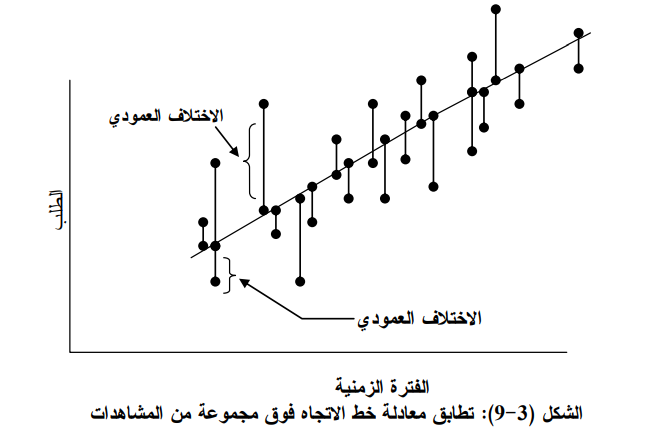
ويتم حساب ثوابت معادلة (3ــ9) باستخدام البيانات المتوفرة عن السلسلة الزمنية بحيث إذا ما رسمت هذه المعادلة فوق نفس البيانات كما في الشكل (3ـ 9) فان الشروط التالية سوف تحقق:
أ ـ مجموع الانحرافات العمودية بين أي نقطة على الرسم و النقطة التي تقابلها على خط الاتجاه يساوي صفرا .
ب ـ مجموع مربع الانحرافات العمودية بين أي نقطة على الرسم و النقطة المقترنة بها على خط الاتجاه يكون أصغر ما يمكن.
ج - خط الاتجاه يمر في الوسط الحسابي البيانات .
وعلى افتراض ان معادلة الاتجاه ذات صيغة خطية، فان ثوابت معادلة خط الاتجاه تُحسب عن طريق حل المعادلتين الطبيعيتين (Normal Equations) التاليتين بطريقة آنية :
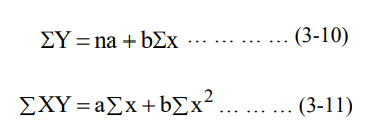
حيث إن: n= عدد المشاهدات في السلسلة الزمنية
ولحل المعادلتين السابقتين فإننا نجد الوسط الفرضي للمتغير (X) أولا، ثم نقوم بطرح قيمة الوسط الفرضي من قيم المتغير (X) وجمع النتائج فيكون حاصل جمع الفرق مساوياً إلى صفر 0 = X£. ويجعل في معادلتي (3-10) (3 ــ 11) تحصل على الصيغة التالية:
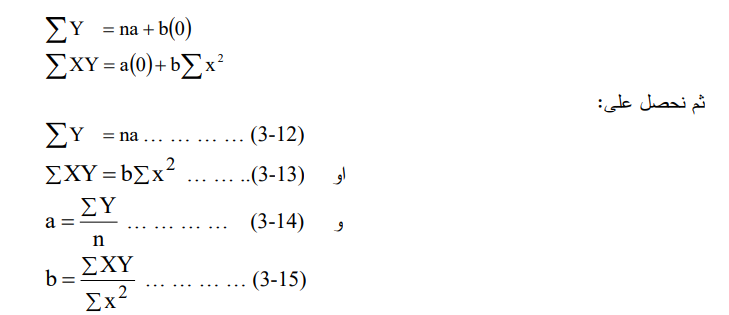
والمثال التالي يوضح كيفية تطبيق هذه الطريقة :
مثال 3 ـ5 :
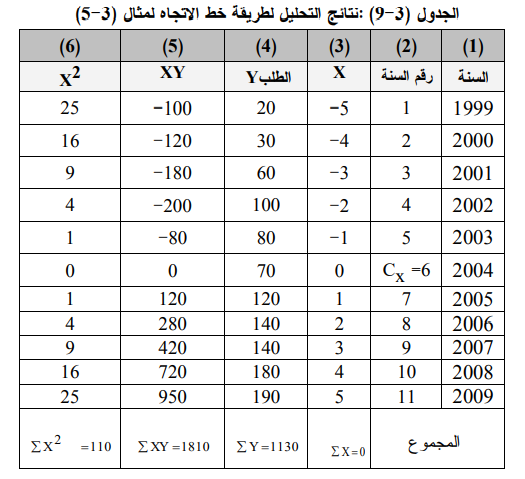
الجدول التالي يبين الطلب على إطارات السيارات من قياس 175 × 13 لدى احدى شركات استيراد وتوزيع الإطارات للأعوام 1999 – 2009 والمطلوب إعداد معادلة خط الاتجاه وتنبؤ الطلب لعام 2010 و 2011 .
الحل /
1ـ نقوم بترقيم السنوات من 1999- 2009 وكما يظهر في الجدول (3-9) عمود (2) .
2ـ نجد قيمة الوسط الفرضي (او المركز) للسلسلة X بالقاعدة الآتية:

3ـ نطرح من رقم كل سنة قيمة الوسط الفرضي فنحصل على النتائج المبينة في الجدول (3-9) عمود (3) .
4ـ نعوض القيم التي حصلنا من الجدول (3-9) في معادلتي (3-10) و(3-11) فنحصل على قيمة a , b كالآتي :
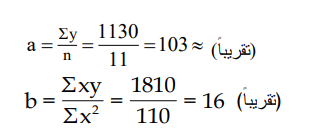
وعلى هذا الاساس فإن معادلة التنبؤ لمثالنا تُكتب بالصيغة التالية :
Y = 103 +16X
وبما ان السنة 2010 والسنة 2011 ستحصلان على رقم 12 و13 على التوالي في السلسلة X فإن تنبؤ الطلب لسنة 2010 يُحسب كالآتي :

إن الرقم 6 الذي حل محل X لا يشير إلى مركز السلسلة X ، وإنما يشير إلى عدد السنوات التي تفرق بين سنة 2010 ومركز السلسلة x الذي يقابل سنة 2004 أي (6 = 2004 - 2010) أو (6 = 6 - 12). وبالنسبة لعام 2011 فان هذا الفرق يبلغ (7) أي (7 =6 - 13).
أما التنبؤ لسنة 2001 فانه يبلغ:
Y13 = 103 + 16(7)
أو 215000 لأن الطلب بالآلاف 215 =
ويمتاز هذا الأسلوب بأنه يأخذ جميع المشاهدات بنظر الاعتبار عند استخراج ثوابت المعادلة الأمر الذي يقلل من اثر العوامل العشوائية. ويعاب عليه بأنه يتطلب مجهوداً حسابياً مطولاً، فضلاً عن أنه يعطي نفس الوزن أو الأهمية لجميع المشاهدات كما انه غير قادر على تحسس الآثار الموسمية التي تؤثر في الطلب.
 الاكثر قراءة في التنبؤ والتخطيط و تحسين الانتاج والعمليات
الاكثر قراءة في التنبؤ والتخطيط و تحسين الانتاج والعمليات
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















