


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 5-11-2020
Date: 30-5-2020
Date: 19-10-2020
|
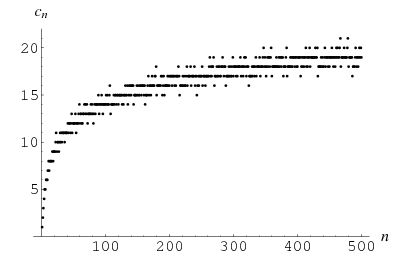
The complexity 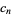 of an integer
of an integer 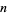 is the least number of 1s needed to represent it using only additions, multiplications, and parentheses. For example, the numbers 1 through 10 can be minimally represented as
is the least number of 1s needed to represent it using only additions, multiplications, and parentheses. For example, the numbers 1 through 10 can be minimally represented as
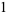 |
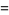 |
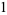 |
(1) |
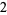 |
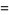 |
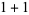 |
(2) |
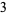 |
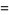 |
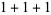 |
(3) |
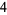 |
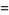 |
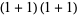 |
(4) |
 |
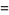 |
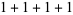 |
(5) |
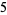 |
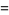 |
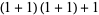 |
(6) |
 |
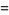 |
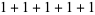 |
(7) |
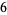 |
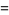 |
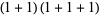 |
(8) |
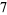 |
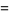 |
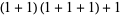 |
(9) |
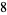 |
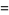 |
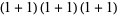 |
(10) |
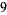 |
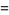 |
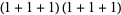 |
(11) |
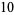 |
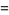 |
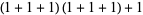 |
(12) |
 |
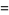 |
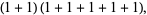 |
(13) |
so the complexities for 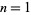 , 2, ..., are 1, 2, 3, 4, 5, 5, 6, 6, 6, 7, 8, 7, 8, ... (OEIS A005245).
, 2, ..., are 1, 2, 3, 4, 5, 5, 6, 6, 6, 7, 8, 7, 8, ... (OEIS A005245).
The smallest numbers of complexity 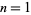 , 2, ... are 1, 2, 3, 4, 5, 7, 10, 11, 17, 22, 23, 41, ... (OEIS A005520).
, 2, ... are 1, 2, 3, 4, 5, 7, 10, 11, 17, 22, 23, 41, ... (OEIS A005520).
REFERENCES:
Guy, R. K. "Expressing Numbers Using Just Ones." §F26 in Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, p. 263, 1994.
Guy, R. K. "Some Suspiciously Simple Sequences." Amer. Math. Monthly 93, 186-190, 1986.
Guy, R. K. "Monthly Unsolved Problems, 1969-1987." Amer. Math. Monthly 94, 961-970, 1987.
Guy, R. K. "Unsolved Problems Come of Age." Amer. Math. Monthly 96, 903-909, 1989.
Pegg, E. Jr. "Math Games: Integer Complexity." Feb. 12, 2004. https://www.maa.org/editorial/mathgames/mathgames_04_12_04.html.
Pegg, E. Jr. "Integer Complexity." https://library.wolfram.com/infocenter/MathSource/5175/.
Rawsthorne, D. A. "How Many 1's are Needed?" Fib. Quart. 27, 14-17, 1989.
Sloane, N. J. A. Sequences A005245/M0457 and A005520/M0523 in "The On-Line Encyclopedia of Integer Sequences."
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 916, 2002.



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ناسا تكتشف "مدينة مهجورة" تحت جليد القطب الشمالي
|
|
|
|
|
|
|
ضمن أسبوع الإرشاد النفسي.. جامعة العميد تُقيم أنشطةً ثقافية وتطويرية لطلبتها
|
|
|