المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Gnomonic Number |
 2192
 05:27 مساءً
date: 12-12-2020 |
Author : Sloane, N. J. A. 
Book or Source : Sequence A005408/M2400 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 22-12-2019
957
Date: 17-1-2021
923
Date: 25-3-2020
771
|
A figurate number of the form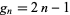 
giving the area of the square gnomon obtained by removing a square of side 
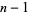from a square of side 
,
 |
 |
 |
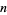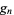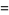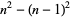(1) |
 |
 |
 |
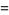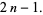(2) |
The gnomonic numbers are therefore equivalent to the odd numbers, and the first few are 1, 3, 5, 7, 9, 11, ... (OEIS A005408). The generating function for the gnomonic numbers is
 |
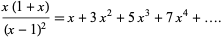(3) |
REFERENCES:
Sloane, N. J. A. Sequence A005408/M2400 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
لخفض ضغط الدم.. دراسة تحدد "تمارين مهمة"
|
|
|
|
|
|
|
طال انتظارها.. ميزة جديدة من "واتساب" تعزز الخصوصية
|
|
|
|
|
|
|
بمناسبة مرور 40 يومًا على رحيله الهيأة العليا لإحياء التراث تعقد ندوة ثقافية لاستذكار العلامة المحقق السيد محمد رضا الجلالي
|
|
|
