


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-10-2020
Date: 17-10-2019
Date: 28-11-2020
|
The tetranacci numbers are a generalization of the Fibonacci numbers defined by 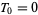 ,
, 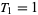 ,
, 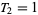 ,
, 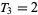 , and the recurrence relation
, and the recurrence relation
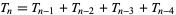 |
(1) |
for 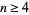 . They represent the
. They represent the 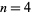 case of the Fibonacci n-step numbers. The first few terms for
case of the Fibonacci n-step numbers. The first few terms for 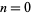 , 1, ... are 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, ... (OEIS A000078).
, 1, ... are 0, 1, 1, 2, 4, 8, 15, 29, 56, 108, 208, ... (OEIS A000078).
The first few prime tetranacci numbers have indices 3, 7, 11, 12, 36, 56, 401, 2707, 8417, 14096, 31561, 50696, 53192, 155182, ... (OEIS A104534), corresponding to 2, 29, 401, 773, 5350220959, ... (OEIS A104535), with no others for 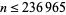 (E. W. Weisstein, Mar. 21, 2009).
(E. W. Weisstein, Mar. 21, 2009).
An exact expression for the 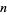 th tetranacci number for
th tetranacci number for 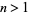 can be given explicitly by
can be given explicitly by
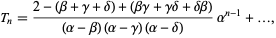 |
(2) |
where the three additional terms are obtained by cyclically permuting 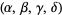 , which are the four roots of the polynomial
, which are the four roots of the polynomial
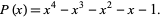 |
(3) |
Alternately,
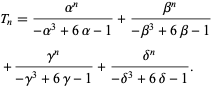 |
(4) |
This can be written in slightly more concise form as
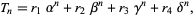 |
(5) |
where 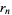 is the
is the 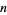 th root of the polynomial
th root of the polynomial
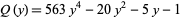 |
(6) |
and 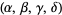 and
and 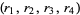 are in the ordering of the Wolfram Language's Root object.
are in the ordering of the Wolfram Language's Root object.
The tetranacci numbers have the generating function
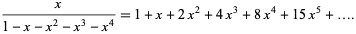 |
(7) |
The ratio of adjacent terms tends to the positive real root of 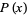 , namely 1.92756... (OEIS A086088), which is sometimes known as the tetranacci constant.
, namely 1.92756... (OEIS A086088), which is sometimes known as the tetranacci constant.
REFERENCES:
Sloane, N. J. A. Sequences A000078/M1108, A086088, A104534, and A104535 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|