


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-10-2020
Date: 1-11-2020
Date: 14-11-2020
|
A positive proper divisor is a positive divisor of a number 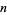 , excluding
, excluding 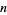 itself. For example, 1, 2, and 3 are positive proper divisors of 6, but 6 itself is not. The number of proper divisors of
itself. For example, 1, 2, and 3 are positive proper divisors of 6, but 6 itself is not. The number of proper divisors of 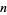 is therefore given by
is therefore given by
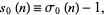 |
where 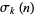 is the divisor function. For
is the divisor function. For 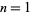 , 2, ...,
, 2, ..., 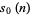 is therefore given by 0, 1, 1, 2, 1, 3, 1, 3, 2, 3, ... (OEIS A032741). The largest proper divisors of
is therefore given by 0, 1, 1, 2, 1, 3, 1, 3, 2, 3, ... (OEIS A032741). The largest proper divisors of 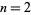 , 3, ... are 1, 1, 2, 1, 3, 1, 4, 3, 5, 1, ... (OEIS A032742).
, 3, ... are 1, 1, 2, 1, 3, 1, 4, 3, 5, 1, ... (OEIS A032742).
The term "proper divisor" is sometimes used to include negative integer divisors of a number 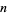 (excluding
(excluding 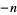 ). Using this definition,
). Using this definition, 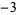 ,
, 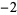 ,
, 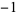 , 1, 2, and 3 are the proper divisors of 6, while
, 1, 2, and 3 are the proper divisors of 6, while 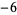 and 6 are the improper divisors.
and 6 are the improper divisors.
To make matters even more confusing, the proper divisor is often defined so that 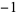 and 1 are also excluded. Using this alternative definition, the proper divisors of 6 would then be
and 1 are also excluded. Using this alternative definition, the proper divisors of 6 would then be 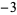 ,
, 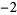 , 2, and 3, and the improper divisors would be
, 2, and 3, and the improper divisors would be 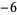 ,
, 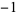 , 1, and 6.
, 1, and 6.
REFERENCES:
Derbyshire, J. Prime Obsession: Bernhard Riemann and the Greatest Unsolved Problem in Mathematics. New York: Penguin, pp. 8-9, 2004.
Sloane, N. J. A. Sequences A032741 and A032742 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
عقد جلسة حوارية عن ضحايا جرائم التطرف ضمن فعاليات اليوم الثاني لمؤتمر ذاكرة الألم
|
|
|