


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 7-8-2020
Date: 16-1-2020
Date: 11-10-2020
|
A number of the form 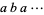 ,
, 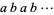 , etc. The first few nontrivial undulants (with the stipulation that
, etc. The first few nontrivial undulants (with the stipulation that 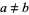 ) are 101, 121, 131, 141, 151, 161, 171, 181, 191, 202, 212, ... (OEIS A046075). Including the trivial 1- and 2-digit undulants and dropping the requirement that
) are 101, 121, 131, 141, 151, 161, 171, 181, 191, 202, 212, ... (OEIS A046075). Including the trivial 1- and 2-digit undulants and dropping the requirement that 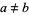 gives OEIS A033619.
gives OEIS A033619.
The first few undulating squares are 121, 484, 676, 69696, ... (OEIS A016073), with no larger such numbers of fewer than a million digits (Pickover 1995). Several tricks can be used to speed the search for square undulating numbers, especially by examining the possible patterns of ending digits. For example, the only possible sets of four trailing digits for undulating squares are 0404, 1616, 2121, 2929, 3636, 6161, 6464, 6969, 8484, and 9696.
The only undulating power 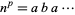 for
for 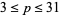 and up to 100 digits is
and up to 100 digits is 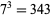 (Pickover 1995). A large undulating prime is given by
(Pickover 1995). A large undulating prime is given by 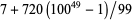 (Pickover 1995).
(Pickover 1995).
A binary undulant is a power of 2 whose base-10 representation contains one or both of the sequences 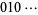 and
and 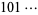 . The first few are
. The first few are 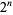 for
for 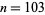 , 107, 138, 159, 179, 187, 192, 199, 205, ... (OEIS A046076). The smallest
, 107, 138, 159, 179, 187, 192, 199, 205, ... (OEIS A046076). The smallest 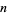 for which an undulating sequence of exactly
for which an undulating sequence of exactly 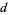 -digit occurs for
-digit occurs for 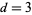 , 4, ... are
, 4, ... are 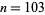 , 138, 875, 949, 6617, 1802, 14545, ... (OEIS A046077). An undulating binary sequence of length 10 occurs for
, 138, 875, 949, 6617, 1802, 14545, ... (OEIS A046077). An undulating binary sequence of length 10 occurs for 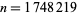 (Pickover 1995).
(Pickover 1995).
REFERENCES:
Pickover, C. A. "Is There a Double Smoothly Undulating Integer?" In Computers, Pattern, Chaos and Beauty. New York: St. Martin's Press, 1990.
Pickover, C. A. "The Undulation of the Monks." Ch. 20 in Keys to Infinity. New York: W. H. Freeman, pp. 159-161 1995.
Sloane, N. J. A. Sequences A016073, A033619, A046075, A046076, and A046077 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|