


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 9-12-2020
Date: 26-10-2020
Date: 19-1-2021
|
The sequence 1, 2, 2, 3, 3, 3, 4, 4, 4, 4, ... (OEIS A002024) consisting of 1 copy of 1, 2 copies of 2, 3 copies of 3, and so on. Surprisingly, there exist simple formulas for the 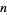 th term
th term 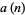 ,
,
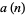 |
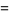 |
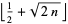 |
(1) |
 |
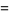 |
![[1/2(sqrt(8n+1)-1)],](https://mathworld.wolfram.com/images/equations/Self-CountingSequence/Inline8.gif) |
(2) |
where 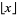 is the floor function and
is the floor function and ![[x]](https://mathworld.wolfram.com/images/equations/Self-CountingSequence/Inline10.gif) is the ceiling function (Graham et al. 1994, p. 97). The sequence is also given by the recursive sequence
is the ceiling function (Graham et al. 1994, p. 97). The sequence is also given by the recursive sequence
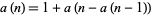 |
(3) |
(Wolfram 2002, p. 129).
REFERENCES:
Gould, H. W. "Solution to Problem 571." Math. Mag. 38, 185-187, 1965.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Exercise 3.23 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, p. 97, 1994.
Sloane, N. J. A. Sequence A002024/M0250 in "The On-Line Encyclopedia of Integer Sequences."Knuth, D. E. The Art of Computer Programming, Vol. 1: Fundamental Algorithms, 3rd ed. Reading, MA: Addison-Wesley, p. 43, 1997.
Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, 129, 2002.



|
|
|
|
للعاملين في الليل.. حيلة صحية تجنبكم خطر هذا النوع من العمل
|
|
|
|
|
|
|
"ناسا" تحتفي برائد الفضاء السوفياتي يوري غاغارين
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|