


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-6-2020
Date: 16-10-2019
Date: 3-8-2020
|
Consider the recurrence equation defined by 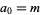 and
and
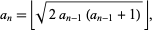 |
(1) |
where 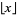 is the floor function. Graham and Pollak actually defined
is the floor function. Graham and Pollak actually defined 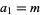 , but the indexing
, but the indexing 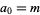 will be used here for convenience, following Borwein and Bailey (2003, p. 62). The first few terms are summarized in the following table for small values of
will be used here for convenience, following Borwein and Bailey (2003, p. 62). The first few terms are summarized in the following table for small values of 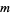 .
.
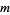 |
OEIS | 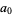 , , 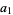 , ... , ... |
| 1 | A001521 | 1, 2, 3, 4, 6, 9, 13, 19, 27, 38, 54, ... |
| 5 | A091522 | 5, 7, 10, 14, 20, 28, 40, 57, 81, 115, ... |
| 8 | A091523 | 8, 12, 17, 24, 34, 48, 68, 96, 136, 193, ... |
Amazingly, an explicit formula for 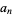 with
with 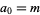 is given by
is given by
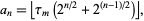 |
(2) |
where 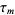 is the
is the 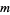 th smallest number in the set
th smallest number in the set 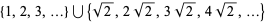 (Graham and Pollak 1970; Borwein and Bailey 2003, p. 63).
(Graham and Pollak 1970; Borwein and Bailey 2003, p. 63).
Now consider the associated sequence
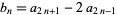 |
(3) |
whose value is always 0 or 1. Even more amazingly, interpreting the sequence 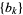 as a series of binary bits gives a series of algebraic constants
as a series of binary bits gives a series of algebraic constants
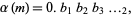 |
(4) |
where the first few constants are
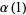 |
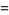 |
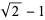 |
(5) |
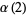 |
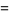 |
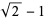 |
(6) |
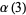 |
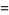 |
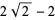 |
(7) |
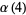 |
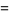 |
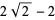 |
(8) |
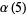 |
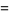 |
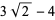 |
(9) |
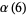 |
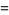 |
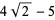 |
(10) |
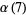 |
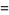 |
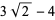 |
(11) |
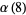 |
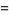 |
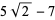 |
(12) |
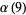 |
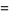 |
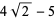 |
(13) |
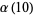 |
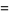 |
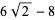 |
(14) |
(OEIS A091524 and A091525; Borwein and Bailey 2003, p. 63).
It is not known if sequences such as
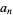 |
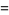 |
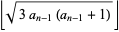 |
(15) |
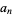 |
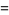 |
![|_RadicalBox[{2, {a, _, {(, {n, -, 1}, )}}, {(, {{a, _, {(, {n, -, 1}, )}}, +, 1}, )}, {(, {{a, _, {(, {n, -, 1}, )}}, +, 2}, )}}, 3]_|](https://mathworld.wolfram.com/images/equations/Graham-PollakSequence/Inline50.gif) |
(16) |
have corresponding properties (Graham and Pollak 1970; Borwein and Bailey 2003, p. 63).
REFERENCES:
Borwein, J. and Bailey, D. Mathematics by Experiment: Plausible Reasoning in the 21st Century. Wellesley, MA: A K Peters, 2003.
Graham, R. L.; Knuth, D. E.; and Patashnik, O. Ex. 3.46 in Concrete Mathematics: A Foundation for Computer Science, 2nd ed. Reading, MA: Addison-Wesley, 1994.
Graham, R. L. and Pollak, H. O. "Note of a Nonlinear Recurrence Related to 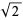 ." Math. Mag. 43, 143-145, 1970.
." Math. Mag. 43, 143-145, 1970.
Guy, R. K. "The Strong Law of Small Numbers." Amer. Math. Monthly 95, 697-712, 1988.
Rabinowitz, S. and Gilbert, P. "A Nonlinear Recurrence Yielding Binary Digits." Math. Mag. 64, 168-171, 1991.
Sloane, N. J. A. Sequences A001521/M0569, A004539, A091522, A091523, A091524, and A091525 in "The On-Line Encyclopedia of Integer Sequences."
Stoll, T. "On Families of Nonlinear Recurrences Related to Digits." J. Integer Sequences 8, No. 05.3.2, 1-8, 2005. https://www.cs.uwaterloo.ca/journals/JIS/VOL8/Stoll/stoll56.pdf.
Stoll, T. "On a Problem of Erdős and Graham Concerning Digits." Acta Arith. 125, 89-100, 2006.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|