المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Hasse-Davenport Relation |
 882
 05:10 مساءً
date: 13-8-2020 |
Author : Ireland, K. and Rosen, M. 
Book or Source : "A Proof of the Hasse-Davenport Relation." §11.4 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag 
Page and Part : pp. 162-165|
Read More
Date: 29-8-2020
616
Date: 12-5-2020
578
Date: 20-11-2020
740
|
Let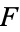 
be a finite field with 
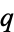elements, and let 
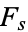be a field containing 
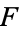such that ![[F_s:F]=s](https://mathworld.wolfram.com/images/equations/Hasse-DavenportRelation/Inline5.gif)
. Let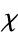 
be a nontrivial multiplicative character of 
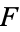and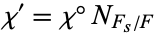 
a character of 
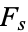. Then
 |
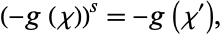where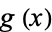 
is a Gaussian sum.
REFERENCES:
Ireland, K. and Rosen, M. "A Proof of the Hasse-Davenport Relation." §11.4 in A Classical Introduction to Modern Number Theory, 2nd ed. New York: Springer-Verlag, pp. 162-165, 1990.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
المجمع العلمي ينظّم ندوة حوارية حول مفهوم العولمة الرقمية في بابل
|
|
|
