المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Erdős-Moser Equation |
 719
 05:54 مساءً
date: 24-5-2020 |
Author : Guy, R. K 
Book or Source : Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994. 
Page and Part : ...|
Read More
Date: 11-11-2019
564
Date: 19-12-2019
536
Date: 1-12-2019
1024
|
The Diophantine equation
 |
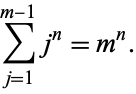Erdős conjectured that there is no solution to this equation other than the trivial solution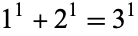 
, although this remains unproved (Guy 1994, pp. 153-154). Moser (1953) proved that there is no solution for 
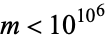, and Butske et al. (1999) extended this to 
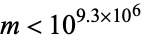, or more specifically, 
.
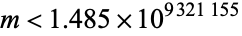REFERENCES:
Butske, W.; Jaje, L. M.; and Mayernik, D. R. "The Equation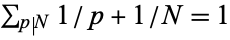 
, Pseudoperfect Numbers, and Partially Weighted Graphs." Math. Comput. 69, 407-420, 1999.
Guy, R. K. Unsolved Problems in Number Theory, 2nd ed. New York: Springer-Verlag, 1994.
Moree, P. "Diophantine Equations of Erdős-Moser Type." Bull. Austral. Math. Soc. 53, 281-292, 1996.
Moser, L. "On the Diophantine Equation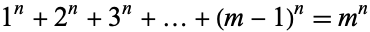 
." Scripta Math. 19, 84-88, 1953.
|
|
|
|
مخاطر عدم علاج ارتفاع ضغط الدم
|
|
|
|
|
|
|
اختراق جديد في علاج سرطان البروستات العدواني
|
|
|
|
|
|
|
مدرسة دار العلم.. صرح علميّ متميز في كربلاء لنشر علوم أهل البيت (عليهم السلام)
|
|
|
