Champernowne Constant Digits

The Champernowne constant has decimal expansion

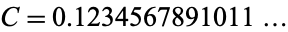(OEIS A033307).

The Earls sequence (starting position of 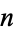 copies of the digit 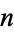) for 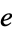 is given for 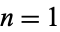, 2, ... by 1, 34, 56, 1222, 1555, 25554, 29998, 433330, 7988888882, 1101010101010, ... (OEIS A224896).

The starting positions of the first occurrence of 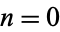, 1, 2, ... in the decimal expansion of  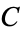(not including the initial 0 to the left of the decimal point) are 11, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 1, ... (OEIS A229186).

Scanning the decimal expansion of 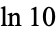 until all 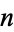-digit numbers have occurred, the last 1-, 2-, ... digit numbers appearing are 0, 00, 000, 0000, ..., which end at digits 11, 192, 2893, 38894, 488895, ... (OEIS A072290).

The digit sequence 0123456789 first occurs at positions 11234567799, 22345677908, 33456779017, 44567790126, 55677901235, 66779012344, ... (OEIS A000000) and 9876543210 at positions 7777777779, 9876543212, 19987654323, 30998765434, 42099876545, 53209987656, 64320998767, ... (OEIS A000000; E. Weisstein, Jul. 26, 2013).

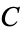-constant primes occur for 10, 14, 24, 235, 2804, 4347, 37735, ... (OEIS A071620) digits.

It is known that the Champernowne constant is normal in base 10 (Champernowne 1933, Bailey and Crandall 2002), though the following table giving the counts of digits in the first 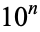 terms shows non-normal behavior up to at least  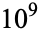due to an excess of 1s and surfeit of 0s when cutting the digit string off at locations such as .

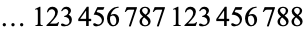	OEIS	10	100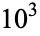
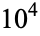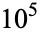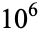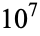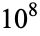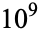0	A000000	0	5	66	747	8642	83528	884151	9234568	96021948
1	A000000	2	16	177	1858	19753	179810	1582562	14234568	130589850
2	A000000	1	16	177	1636	11111	94539	995260	10345679	100589849
3	A000000	1	16	148	858	8642	94539	995161	10234568	96589849
4	A000000	1	16	77	858	8642	94539	995160	9345679	96089849
5	A000000	1	11	77	858	8642	93723	982462	9345679	96029849
6	A000000	1	5	77	858	8642	93538	895160	9345679	96022849
7	A000000	1	5	67	833	8642	93538	894462	9345679	96022049
8	A000000	1	5	67	747	8642	88718	891462	9333333	96021959
9	A000000	1	5	67	747	8642	83528	884160	9234568	96021949

REFERENCES:

Champernowne, D. G. "The Construction of Decimals Normal in the Scale of Ten." J. London Math. Soc. 8, 1933.

Bailey, D. H. and Crandall, R. E. "Random Generators and Normal Numbers." Exper. Math. 11, 527-546, 2002.

Sloane, N. J. A. Sequences A071620, A072290, A224896, and A229186 in "The On-Line Encyclopedia of Integer Sequences."