Negadecimal

The negadecimal representation of a number 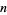 is its representation in base  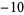(i.e., base negative 10). It is therefore given by the coefficients  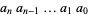in

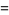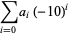			(1)
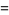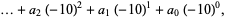			(2)

where 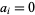, 1, ..., 9.

The negadecimal digits may be obtained with the Wolfram Language code

  Negadecimal[0] := {0}
  Negadecimal[i_] := Rest @ Reverse @
     Mod[NestWhileList[(# - Mod[#, 10])/-10&,
       i, # != 0& ], 10]

The following table gives the negadecimal representations for the first few integers (A039723).

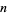	negadecimal		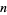negadecimal		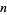negadecimal
1	1	11	191	21	181
2	2	12	192	22	182
3	3	13	193	23	183
4	4	14	194	24	184
5	5	15	195	25	185
6	6	16	196	26	186
7	7	17	197	27	187
8	8	18	198	28	188
9	9	19	199	29	189
10	190	20	180	30	170

The numbers having the same decimal and negadecimal representations are those which are sums of distinct powers of 100: 1, 2, 3, 4, 5, 6, 7, 8, 9, 100, 101, 102, 103, 104, 105, 106, 107, 108, 109, 200, ... (OEIS A051022).

REFERENCES:

Sloane, N. J. A. Sequences A039723 and A051022 in "The On-Line Encyclopedia of Integer Sequences."