Solidus

The diagonal slash "/" used as the bar between numerator and denominator of an in-line fraction (Bringhurst 1997, p. 284). The solidus is also called a diagonal.

Special care is needed when interpreting the meaning of a solidus in in-line math because of the notational ambiguity in expressions such as 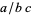. Whereas in many textbooks, "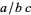" is intended to denote 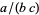, taken literally or evaluated in a symbolic mathematics languages such as the Wolfram Language, it means 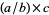. For clarity, parentheses should therefore always be used when delineating compound denominators.

Common examples of failure to parenthesize include 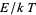 (where  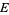is energy,  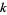is Boltzmann's constant, and  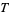is temperature; Arfken 1985, p. 950), its variant  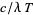(where  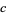is a constant and  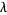is wavelength; Weast 1981, pp. F-109 and F-111), the exponent  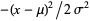in the normal distribution (where  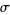is the standard deviation; Hastings 2000, p. 217). Other miscellaneous examples occur even in the standard references for computer math systems (e.g., Wolfram 2003, pp. 776, 779, and 787).

REFERENCES:

Arfken, G. Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, 1985.

Bringhurst, R. The Elements of Typographic Style, 2nd ed. Point Roberts, WA: Hartley and Marks, p. 284, 1997.

Grossman, J. (Managing Ed.). "Solidus." §5.122 in The Chicago Manual of Style, 14th ed. Chicago, IL: University of Chicago Press, p. 189, 1993.

Hastings, K. Introduction to Probability with Mathematica. Boca Raton: Chapman & Hall/CRC, 2000.

Weast, R. C. (Ed.). Handbook of Chemistry and Physics, 61st ed. Boca Raton, FL: CRC Press, 1981.

Wolfram, S. The Mathematica Book, 5th ed. Champaign, IL: Wolfram Media, 2003.